Régression et descente de gradient

Introduction

Dans un article précédent, nous avons vu les principes de la différenciation automatique et l’algorithme du gradient.

Nous allons voir ici des exemples d’applications.

Dérivée automatique

Code

import warnings
from functools import partial

warnings.simplefilter("ignore")

import jax
import jax.numpy as jnp
from jax import grad, jit, vmap
from jax import random
from jax.random import PRNGKey
import matplotlib.pyplot as plt
from jax.experimental import optimizers

plt.style.use("ggplot")
plt.rcParams["figure.figsize"] = (13, 8)

Avec un moteur de différenciation automatique comme JAX, on peut calculer les dérivées d’une fonction arbitraire. Prenons le cas de la fonction qui donne le carré de la norme d’un vecteur en deux dimensions. On peut visualiser les valeurs prises par cette fonction avec une surface. La norme du gradient est proportionnelle à l’inclinaison de la surface dans la direction de plus grande pente ; c’est donc la généralisation de la pente en une dimension.

Code

def make_gradient_field(
    function, xrange=(-1, 2), yrange=(-1, 2), n_points=30, shape=(2, 1)
):
    W = jnp.linspace(*xrange, n_points)
    B = jnp.linspace(*yrange, n_points)
    U, V = jnp.meshgrid(W, B)
    pairs = jnp.dstack([U, V]).reshape(-1, *shape)

    vectorized_fun = jit(vmap(function))
    Z = vectorized_fun(pairs).reshape(n_points, n_points)

    grad_fun = jit(vmap(grad(function)))
    gradvals = grad_fun(pairs)

    gradx = gradvals[:, 0].reshape(n_points, n_points)
    grady = gradvals[:, 1].reshape(n_points, n_points)

    gradnorm = jnp.sqrt(gradx**2 + grady**2)

    return U, V, Z, pairs, gradvals, gradx, grady, gradnorm


def plot_surface(U, V, Z, gradnorm, fig, ax, alpha=0.5, cmap=plt.cm.YlGn):
    scamap = plt.cm.ScalarMappable(cmap=cmap)
    fcolors = scamap.to_rgba(gradnorm)

    surf = ax.plot_surface(U, V, Z, facecolors=fcolors, cmap=cmap, alpha=alpha)

    clb = fig.colorbar(scamap)
    clb.ax.set_title("Norme du gradient")


def plot_quiver(U, V, gradx, grady, gradnorm, ax, cmap=plt.cm.YlGn):
    q = ax.quiver(U, V, gradx, grady, gradnorm, cmap=cmap)
    clb = fig.colorbar(q)
    clb.ax.set_title("Norme du gradient")
    return ax


def fun(v):
    #     return jnp.sin(jnp.sqrt(v[0] ** 2 + v[1] ** 2))
    return jnp.sum(v**2)


U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    fun, (-5, 5), (-5, 5), 30, (2,)
)

fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, gradnorm, fig=fig, ax=ax, alpha=0.7)
plt.xlabel("x")
plt.ylabel("y")
ax.set_zlabel("z")
plt.title("Valeurs prises par la fonction réelle f")
plt.show()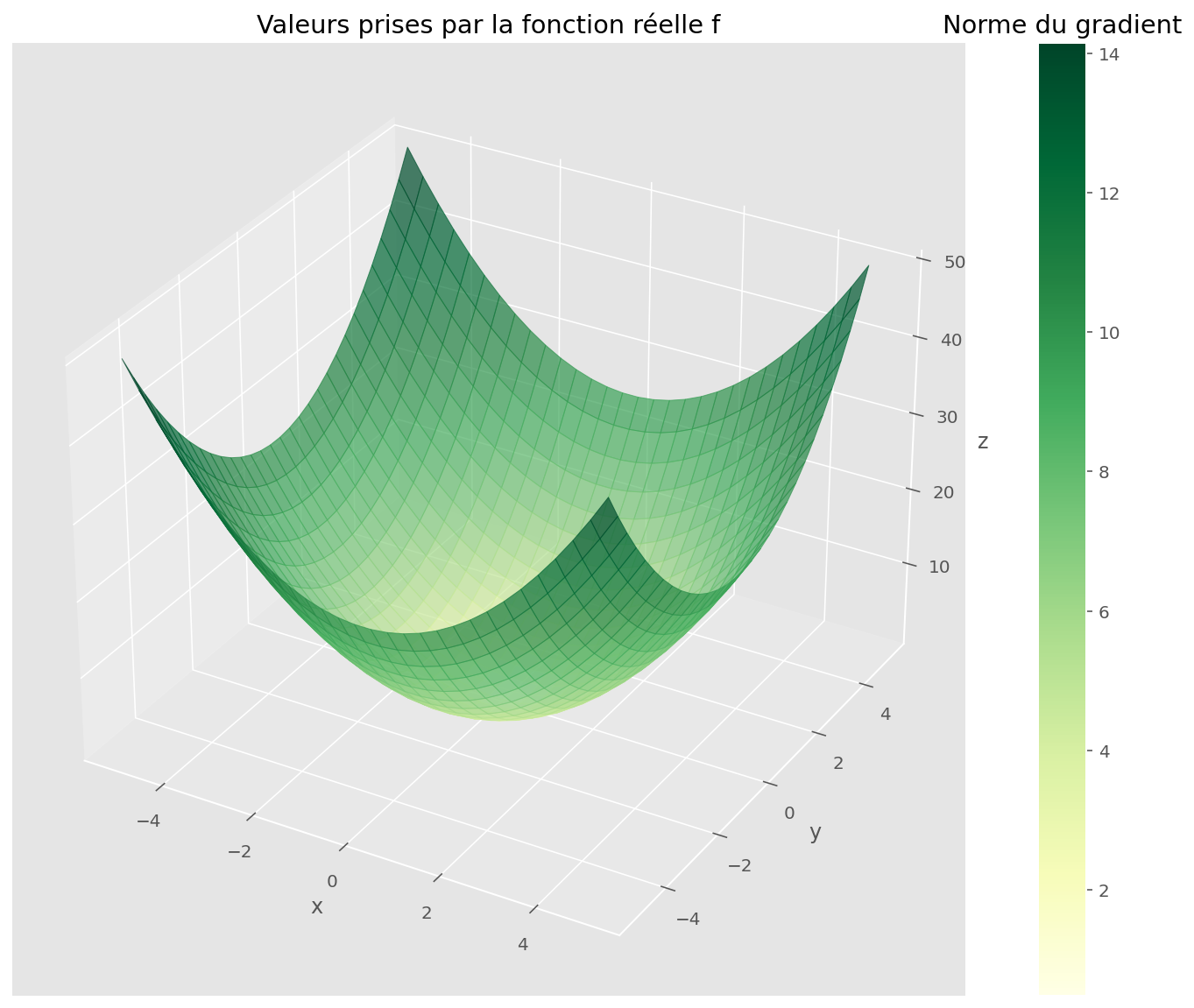

Algorithme de descente

Pour minimiser une fonction, c’est-à-dire trouver un minimum, en sachant uniquement évaluer cette fonction en un point donné, on peut appliquer l’algorithme de la descente de gradient. On part d’un point aléatoire, et on se dirige dans la direction inverse au gradient, proportionnellement à sa norme.

Si la fonction a de bonnes propriétés, on va trouver un minimum.

Code

def gradient_descent(function, init, max_iter=10, lr=0.2):
    grad_fun = jit(grad(function))
    memo = []
    x = init
    for _ in range(max_iter):
        memo.append(x)
        new_x = x - lr * grad_fun(x)
        x = new_x
    return jnp.asarray(memo)


def plot_gradient_descent(params, ax, alpha=1.0):
    ax.scatter(params[:, 0], params[:, 1], c="darkblue", alpha=alpha)
    for i in range(len(params)):
        ax.annotate(
            "",
            xy=params[i + 1],
            xytext=params[i],
            arrowprops={"arrowstyle": "->", "color": "r", "lw": 2, "alpha": alpha},
            va="center",
            ha="center",
        )


memo = gradient_descent(fun, init=jnp.asarray([4.0, 4.0]))

fig, ax = plt.subplots(figsize=(13, 10))

plot_quiver(U, V, gradx, grady, gradnorm, ax=ax)
plot_gradient_descent(memo, ax=ax)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Champ vectoriel du gradient de la fonction f\net descente de gradient")
plt.show()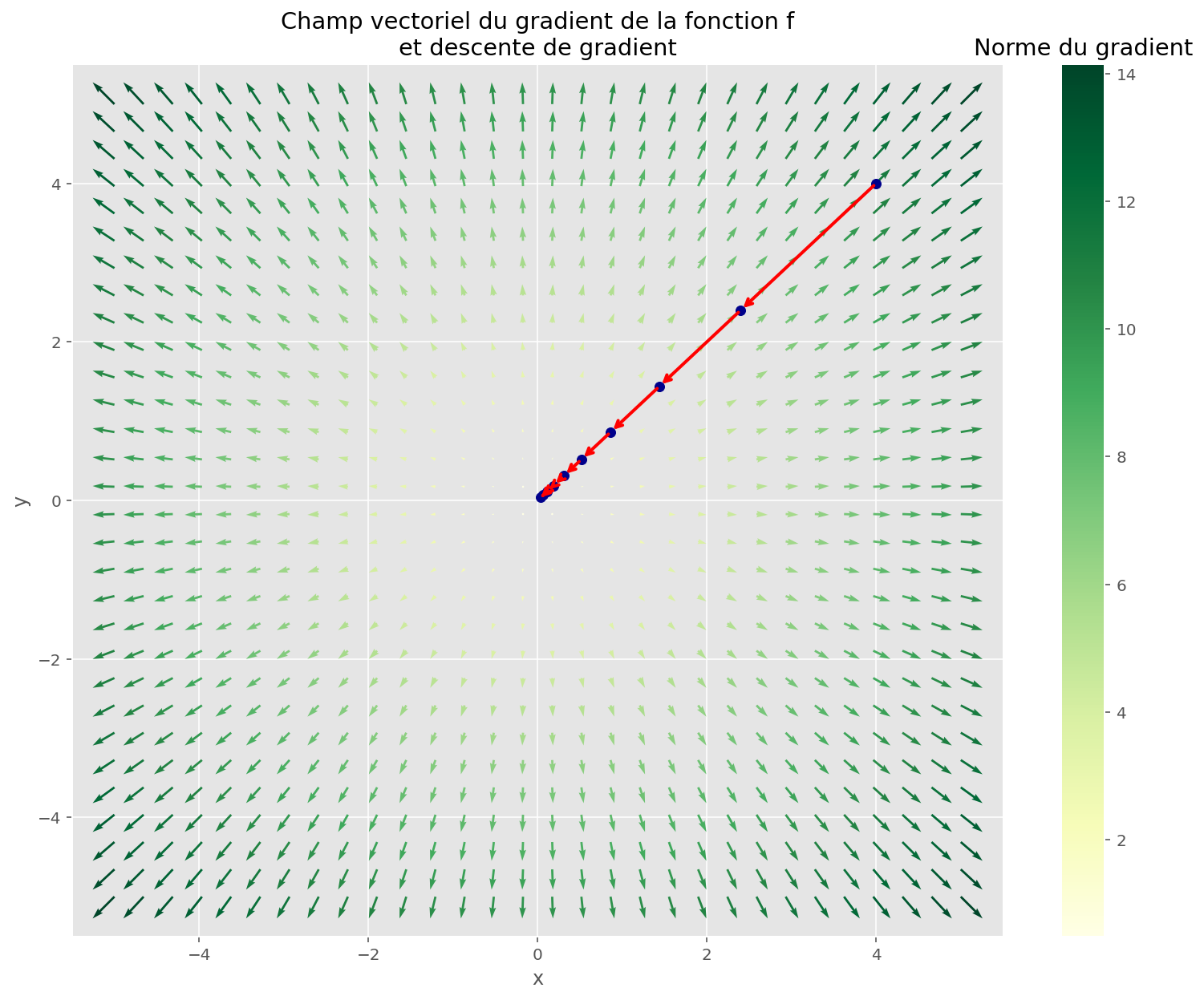

Régression

Nous allons résoudre des tâches de régression avec l’algorithme de descente du gradient. JAX calcule automatiquement le gradient pour nous, il ne nous reste qu’à implémenter l’algorithme de descente.

Régression linéaire

On s’intéresse à un problème en basse dimension: une feature, une cible et 100 observations.

Code

def make_linear_regression(key, n, p):
    key1, key2, key3 = random.split(key, 3)
    x = random.normal(key1, [n, p])
    w = random.normal(key2, [p])
    b = random.normal(key3)
    noise = 0.5 * random.normal(key3, [n])

    # actual data generation process
    y = x @ w + b + noise
    return x, y, w, b


N = 100
P = 1

x, y, w_true, b_true = make_linear_regression(PRNGKey(0), N, P)

fig, ax = plt.subplots(figsize=(13, 10))
plt.scatter(x, y)
plt.title("Problème de régression")
plt.xlabel("Feature")
plt.ylabel("Cible")
plt.show()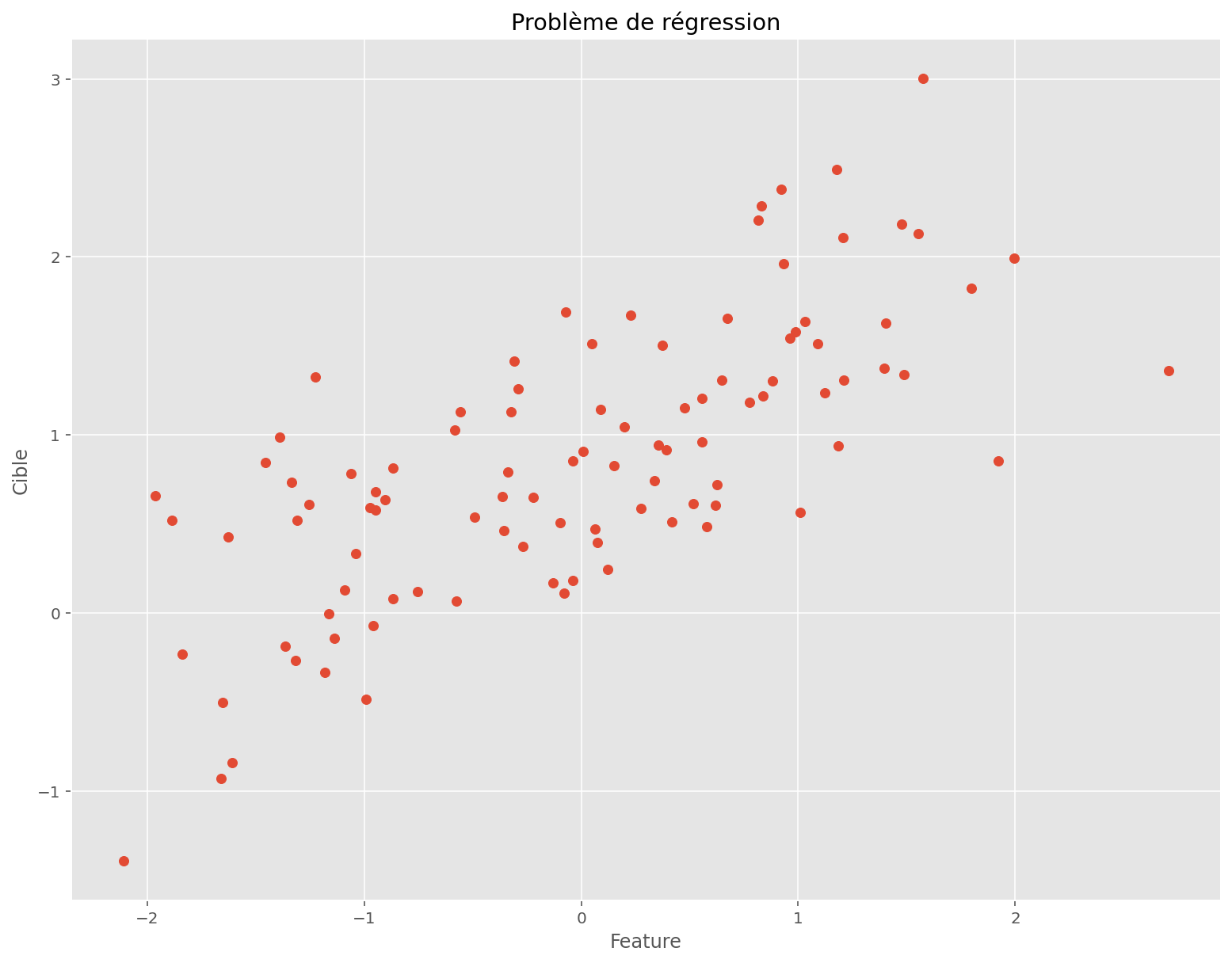

On va entraîner un modèle linéaire pour apprendre à prédire la cible en fonction de l’unique feature.

Pour chaque point de notre jeu d’entraînement, le modèle fait une prédiction. En comparant cette prédiction à la cible (la “vraie” valeur), on obtient un écart.

Nous allons prendre une métrique classique pour les problèmes de régression, c’est-à-dire la mse, soit la moyenne des carrés des écarts.

Notre modèle linéaire possède deux paramètres: le coefficient directeur de la droite, le poids, et l’ordonnée à l’origine, le biais. Il s’agit de trouver automatiquement les paramètres qui vont minimiser notre métrique.

Pour ce faire, on initialise les paramètres au hasard, puis on applique la descente du gradient en minimisant une fonction de coût (ou erreur, ou encore risque). Ici, on va minimiser directement notre métrique ; la fonction de coût et la métrique sont donc identiques.

Code

def init_fn(key, n_features):
    key1, key2 = random.split(key)
    w = random.normal(key1, [n_features])
    b = random.normal(key2)
    return w, b


def linear_apply_fn(params, x):
    w, b = params
    return x @ w + b


# just-in-time compilation, ignore function argument
@partial(jit, static_argnums=0)
def make_loss(apply_fn, params, x, y):
    return jnp.mean((apply_fn(params, x) - y) ** 2)


linear_loss = jit(partial(make_loss, linear_apply_fn))
grad_linear_loss = jit(grad(linear_loss))
# linear_loss_and_grad = jit(jax.value_and_grad(linear_loss))


@partial(jit, static_argnums=(0, 1))
def train(loss, size, initial_params, x, y, lr=0.1):
    grad_loss = jit(grad(loss))

    def scan_fn(params, _):
        current_loss = loss(params, x, y)
        current_grad = grad_loss(params, x, y)

        # gradient descent step
        params = jax.tree_multimap(
            lambda val, grd: val - lr * grd,
            params,
            current_grad,
        )
        return params, jnp.hstack([current_loss, *params, *current_grad])

    params, memo = jax.lax.scan(scan_fn, initial_params, jnp.arange(size))
    return params, memo


def plot_train(apply_fn, initial_params, x, y, memo, params):
    _ = plt.subplots()
    plt.scatter(x, apply_fn(initial_params, x), c="darkblue", label="prédit")
    plt.scatter(x, y, c="red", label="réel")
    plt.legend()
    plt.title("Initialisation de la prédiction avec des paramètres aléatoires")
    plt.xlabel("Feature")
    plt.ylabel("Cible")

    _ = plt.subplots()
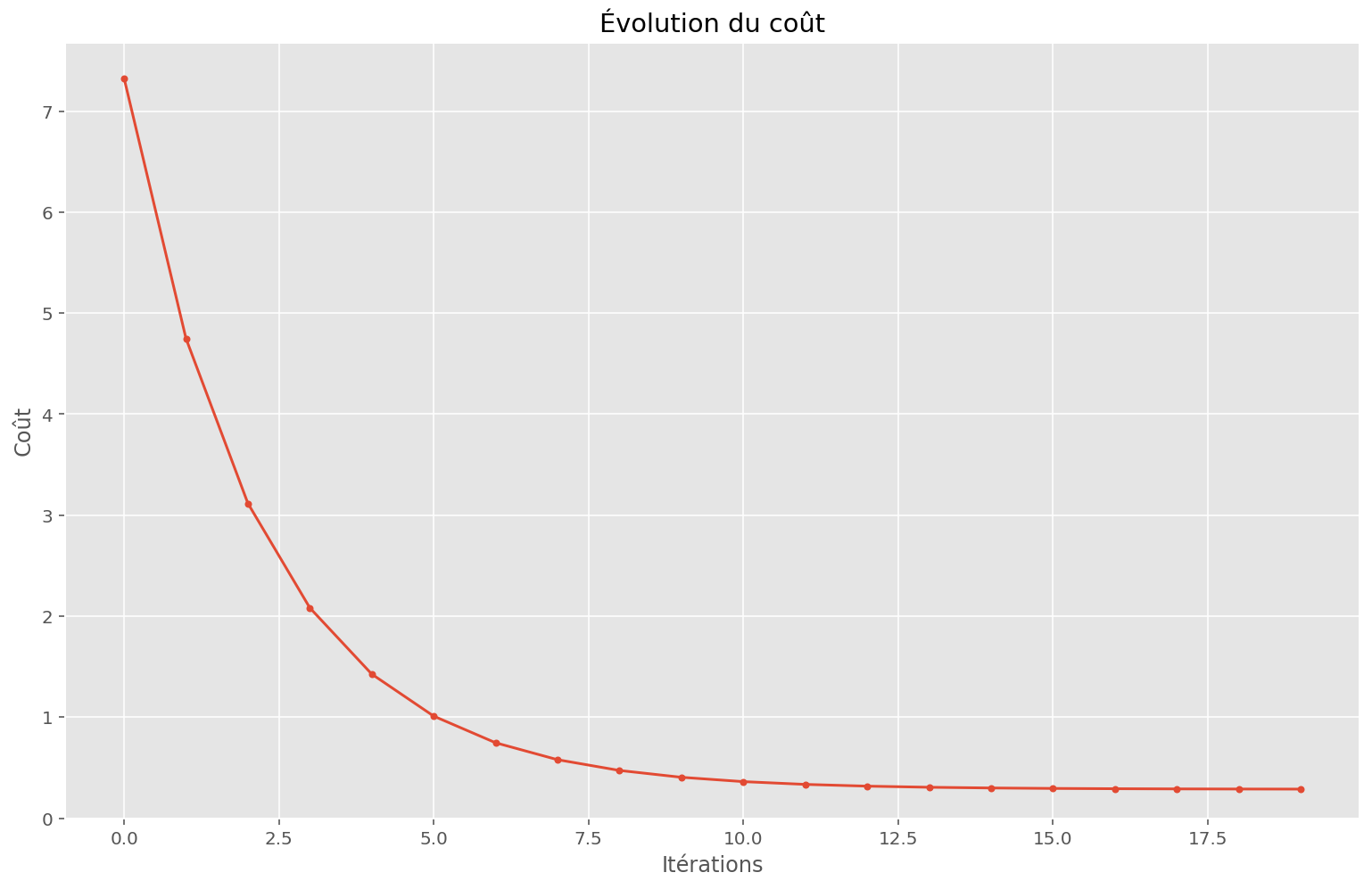
    plt.plot(memo[:, 0], marker=".")
    plt.ylim(0)
    plt.title("Évolution du coût")
    plt.xlabel("Itérations")
    plt.ylabel("Coût")
    print(f"Coût initial: {memo[0, 0]:.2f}")
    print(f"Coût final: {memo[-1, 0]:.2f}")

    _ = plt.subplots()
    plt.scatter(x, apply_fn(params, x), c="darkblue", label="prédiction")
    plt.scatter(x, y, c="red", label="actual")
    plt.legend()
    plt.title("Predictions")
    plt.xlabel("Feature")
    plt.ylabel("Cible")


n_train = 20
initial_params = init_fn(PRNGKey(1), P)
params, memo = train(
    linear_loss,
    n_train,
    initial_params,
    x,
    y,
)
w_found, b_found = params
print(
    f"Paramètres 'vrais': {w_true[0]:.3f}, {b_true:.3f}",
    f"Paramètres trouvés: {w_found[0]:.3f}, {b_found:.3f}",
    sep="\n",
)


plot_train(linear_apply_fn, initial_params, x, y, memo, params)

Paramètres 'vrais': 0.578, 0.854
Paramètres trouvés: 0.516, 0.850
Coût initial: 7.33
Coût final: 0.29

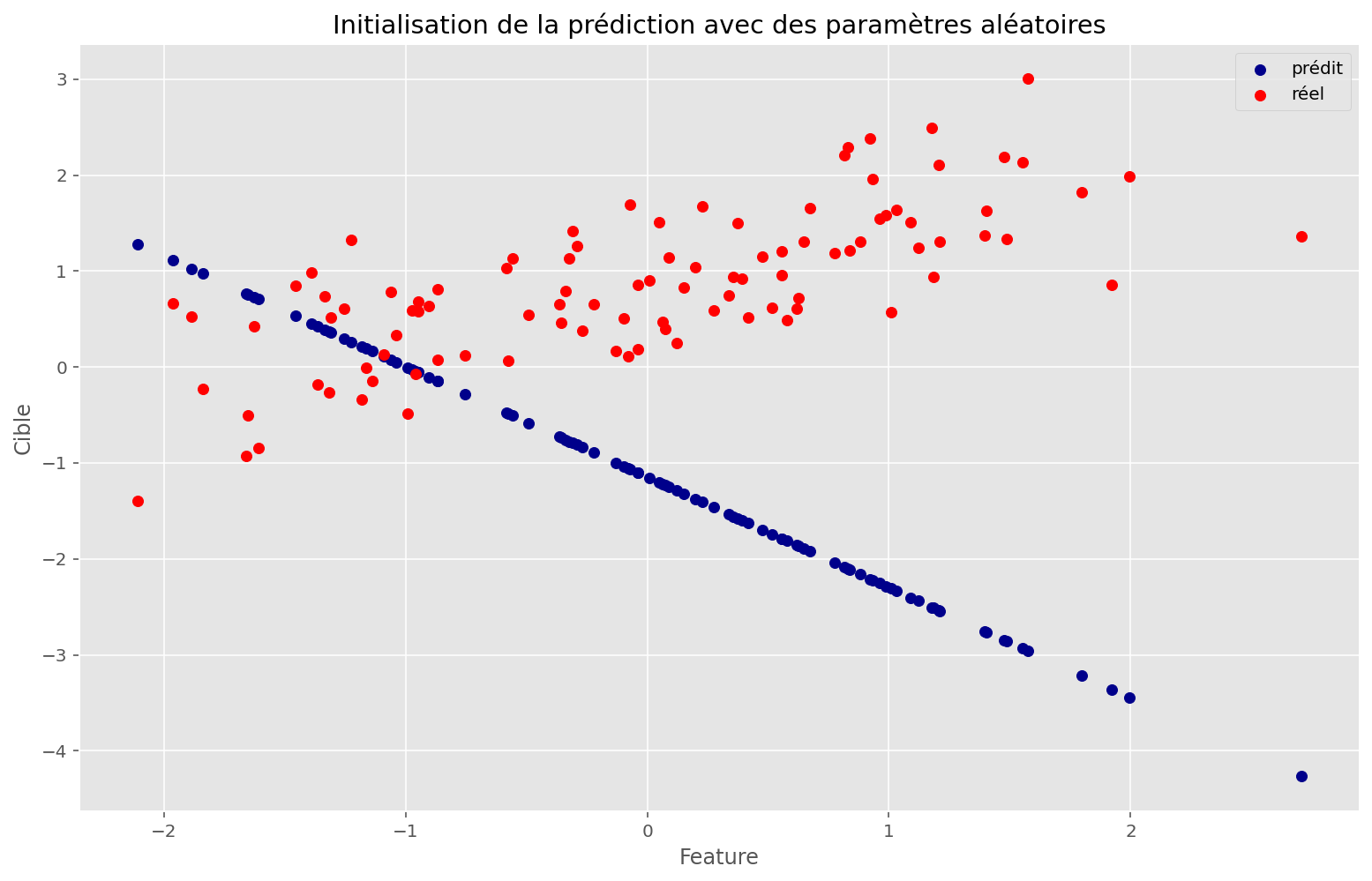
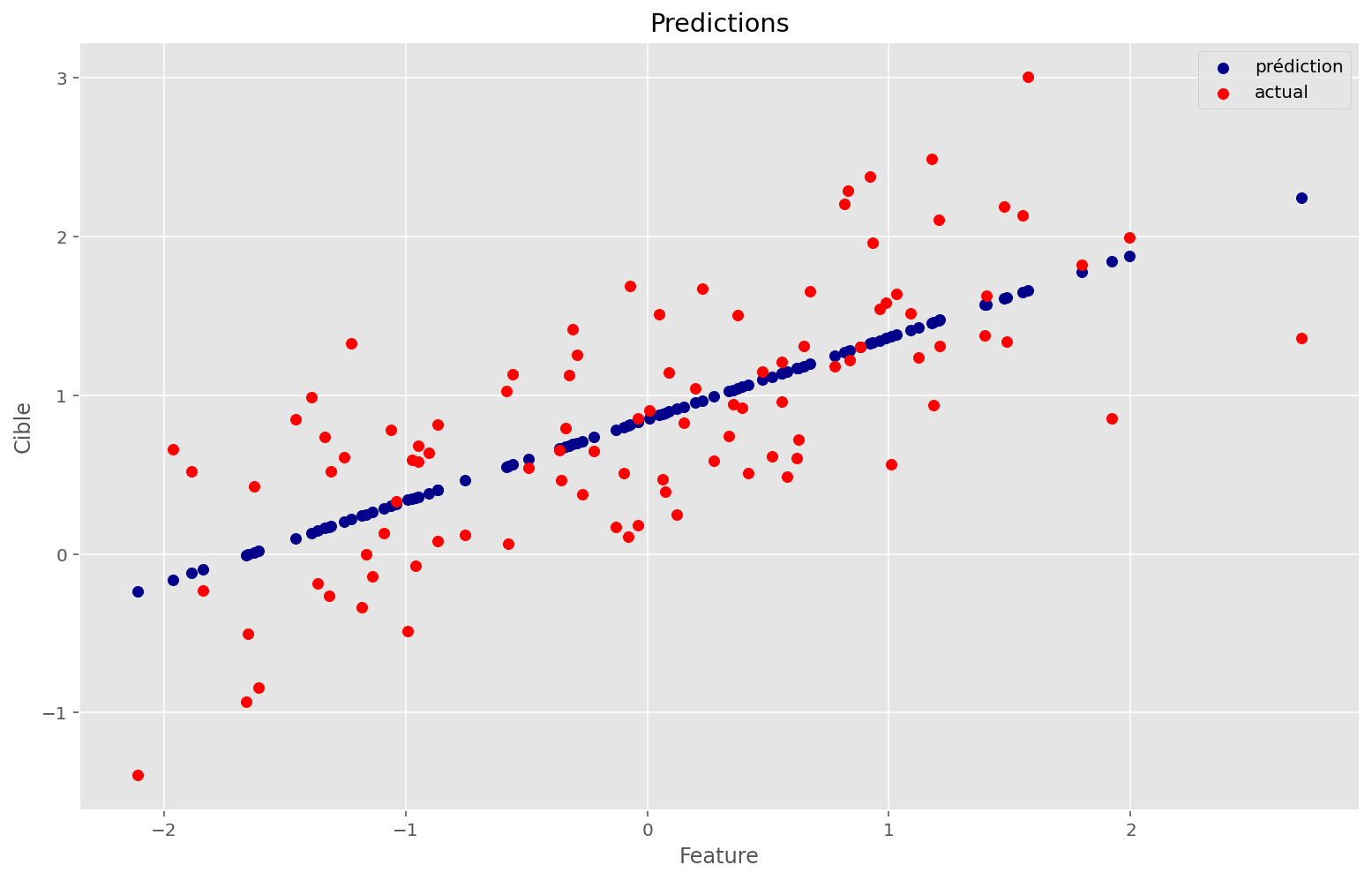
Cette technique a l’air de bien fonctionner: en effet, on retrouve des paramètres très proches de ceux qui nous ont servi à créer ce problème synthétitque.

On peut se demander à quoi ressemble la fonction de coût par rapport à nos deux paramètres. Cela se visualise bien car il y a deux paramètre scalaires, donc nous sommes en dimension 2 (x et y). La troisième dimension z est la valeur de la fonction de coût en chaque point (x, y).

Code

U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    partial(linear_loss, x=x, y=y)
)

fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, gradnorm, fig, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")
ax.set_zlabel("Coût")
plt.title("Coût en fonction des paramètres")

fig, ax = plt.subplots(figsize=(13, 10))
plot_quiver(U, V, gradx, grady, gradnorm, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")

plot_gradient_descent(memo[:, 1:3], ax=ax)
plt.title("Champ vectoriel du gradient\net algorithme de descente")
plt.show()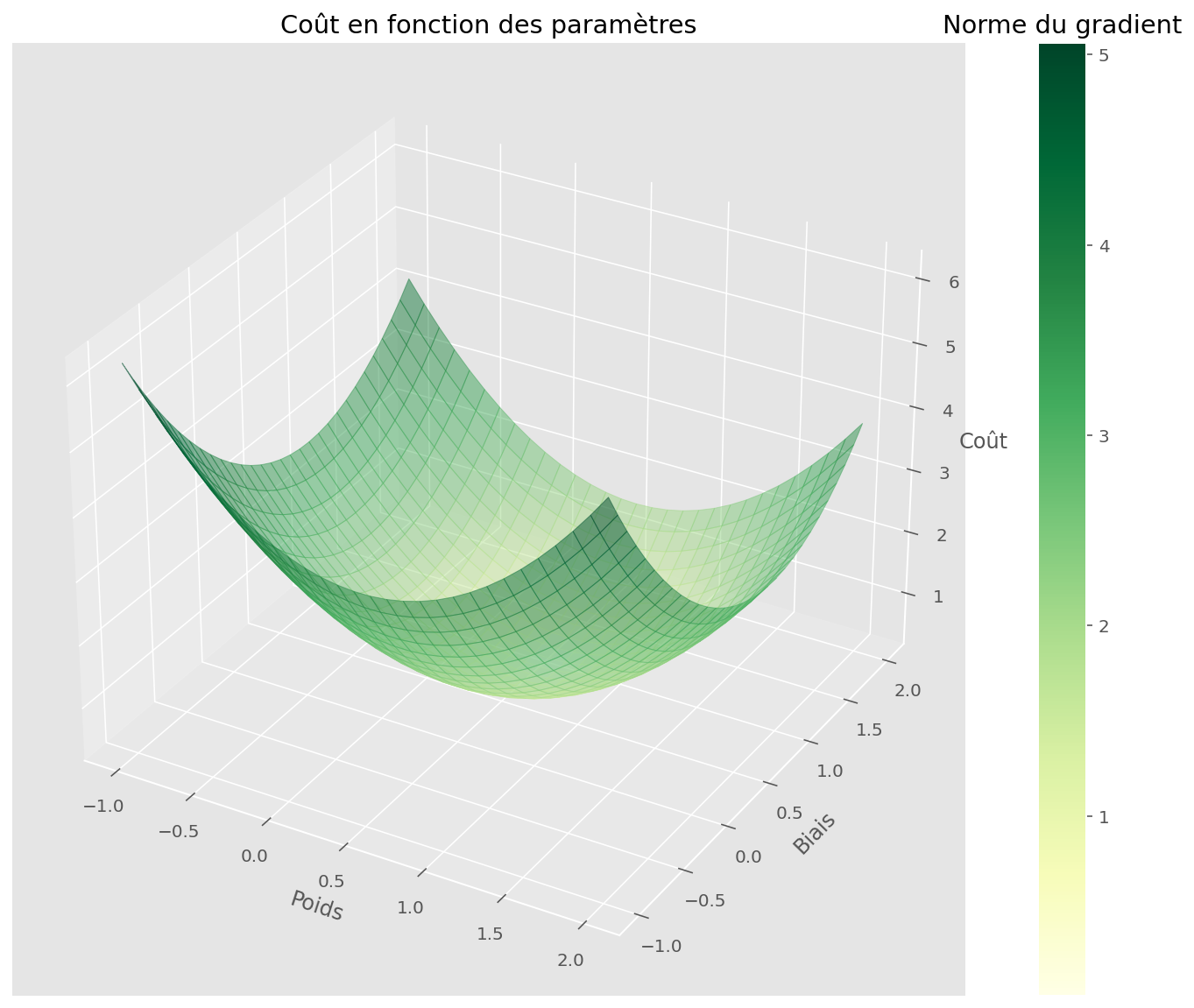

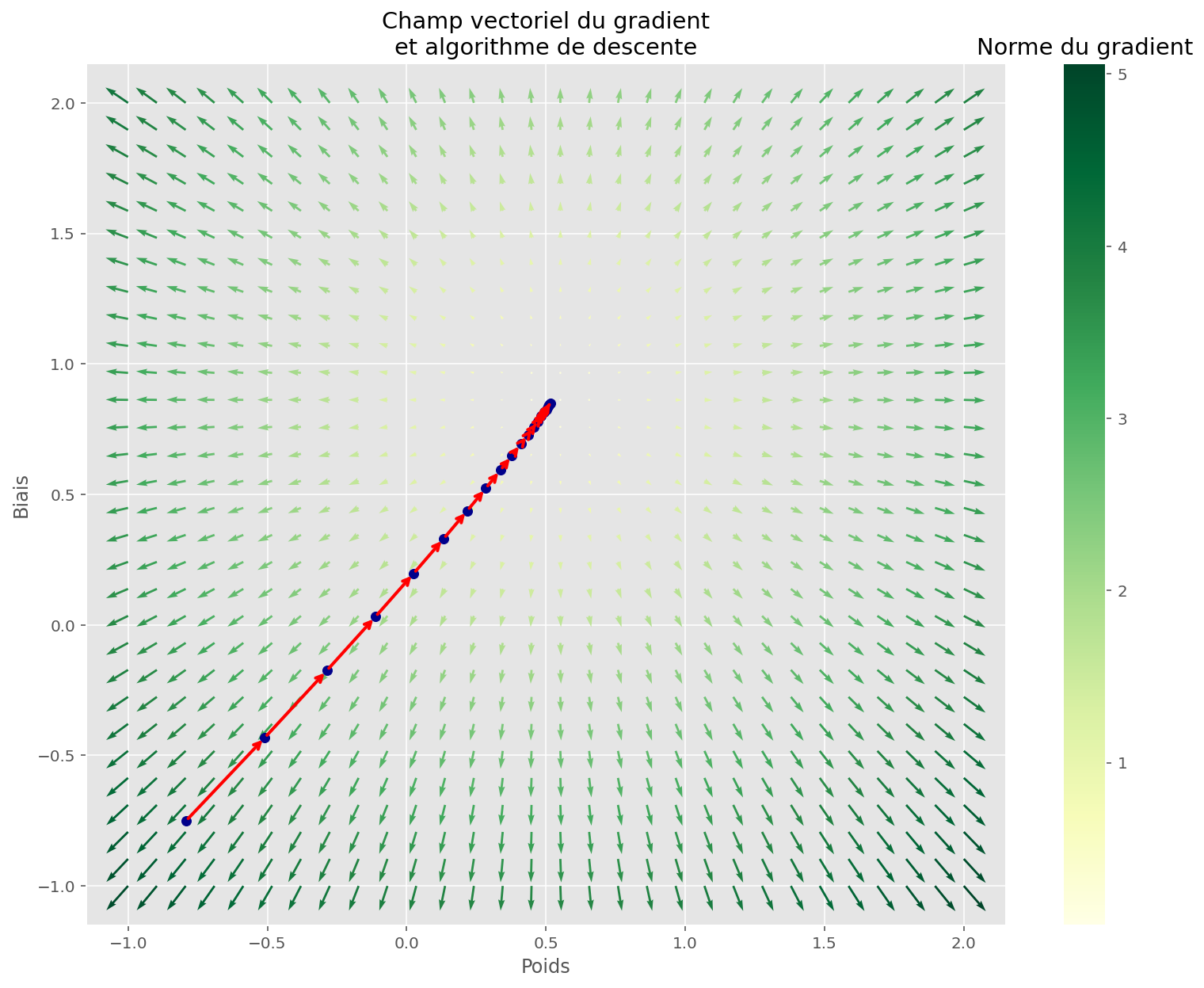
On peut voir que la tâche est simple pour notre algorithme : il suffit en effet de suivre la direction de plus grande pente pour tomber rapidement sur un minimiseur de la fonction de coût.

Descente et inertie

La descente ci-dessus a le mérite de fonctionner ici, mais ce n’est pas tout le temps le cas. En effet, dans le cas où il existe des minima locaux, l’algorithme peut rester bloqué dans une configuration sous-optimale.

Pour améliorer l’algorithme, on peut s’inspirer des lois de la physiques : une bille qui tombe dans une cuvette possède une inertie (momentum), qui va la faire remonter un peu moins haut de l’autre côté, puis redescendre, etc.

Cette variante de l’algorithme initial est bien connue des chercheurs, et fonctionne mieux que l’original pour les problème plus complexes ¹.

Code

@partial(jit, static_argnums=(0, 1, 2))
def train_opt(loss_fn_xy, opt_triple, size, initial_params):
    opt_init, opt_update, get_params = opt_triple
    init_opt_state = opt_init(initial_params)

    def step(step, opt_state):
        loss, grads = jax.value_and_grad(loss_fn_xy)(get_params(opt_state))
        opt_state = opt_update(step, grads, opt_state)
        return loss, opt_state

    def scan_fn(opt_state, i):
        loss, opt_state = step(i, opt_state)
        return opt_state, {"loss": loss, "params": get_params(opt_state)}

    opt_state, losses = jax.lax.scan(scan_fn, init_opt_state, jnp.arange(size))
    return get_params(opt_state), losses


params, memo = train_opt(
    partial(linear_loss, x=x, y=y),
    optimizers.momentum(0.3, 0.7),
    n_train,
    initial_params,
)

U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    partial(linear_loss, x=x, y=y)
)

fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, gradnorm, fig, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")
ax.set_zlabel("Coût")
plt.title("Coût en fonction des paramètres")

fig, ax = plt.subplots(figsize=(13, 10))
plot_quiver(U, V, gradx, grady, gradnorm, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")

memo_params = jnp.dstack(jax.tree_map(jnp.ravel, memo["params"]))[0]
plot_gradient_descent(memo_params, ax=ax)
plt.title("Champ vectoriel du gradient\net algorithme de descente avec inertie")
plt.show()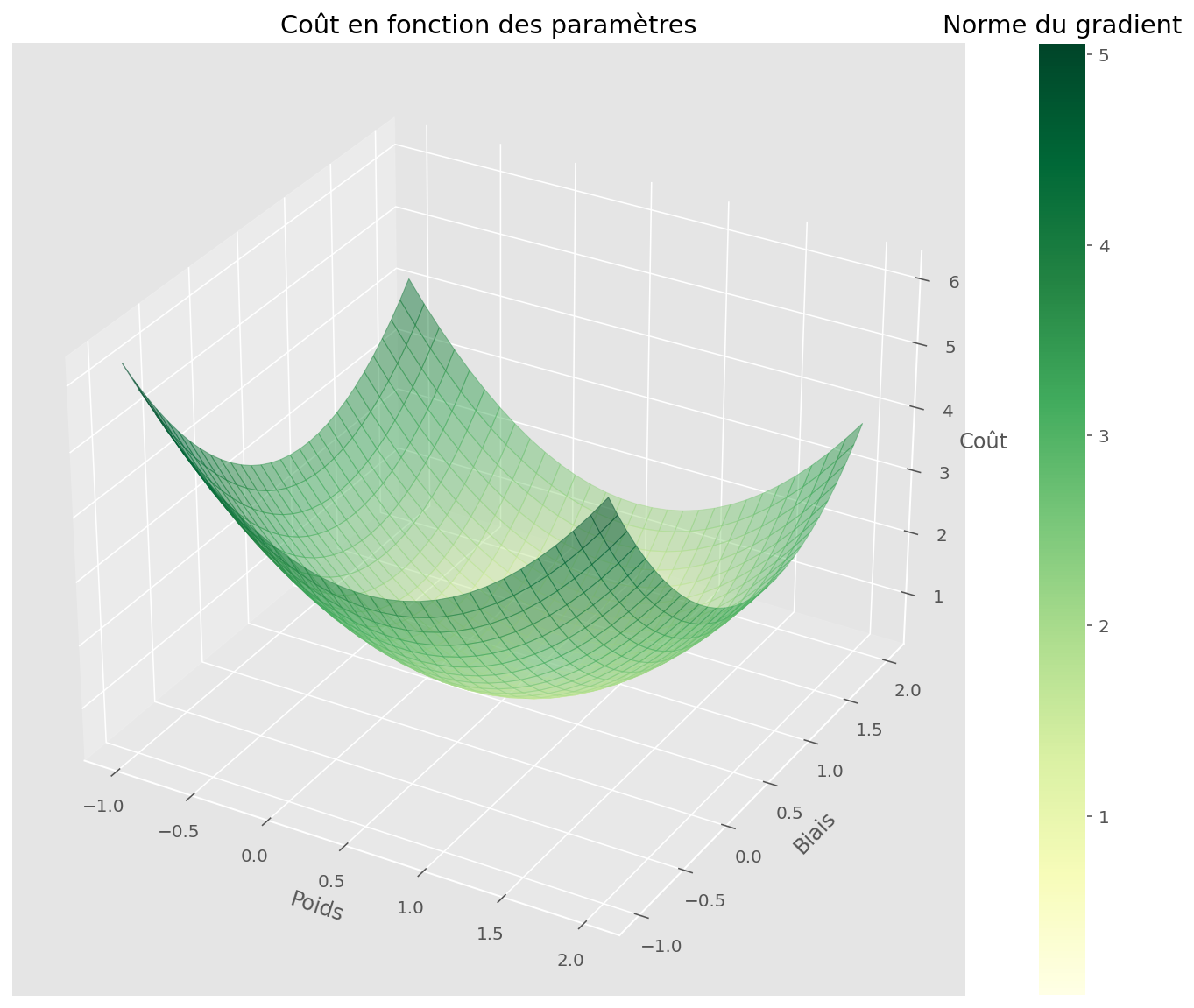

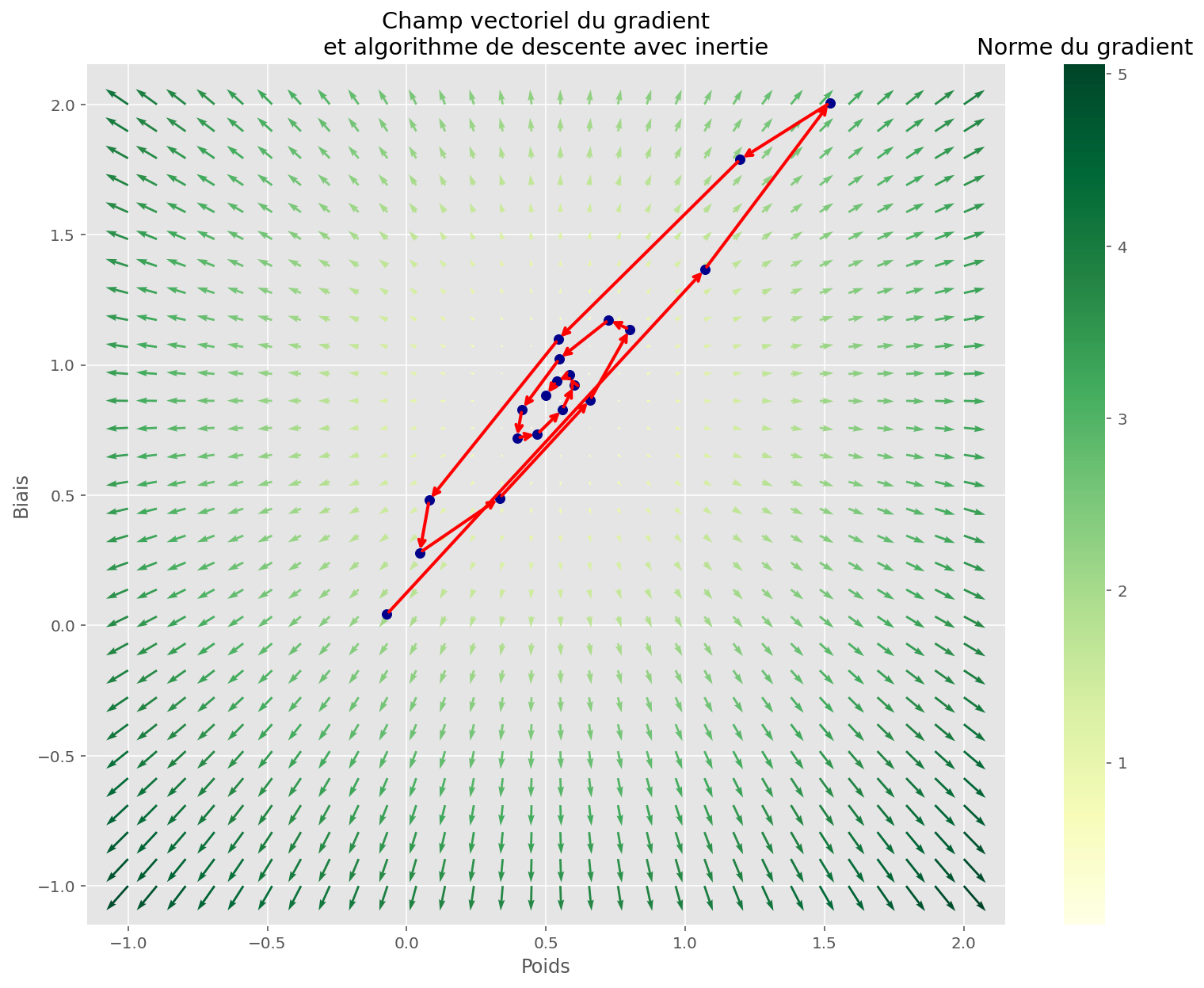
Cet exemple de régression linéaire est utile pour comprendre, mais peu utilisé en pratique. En effet, pour un problème linéaire on peut simplement calculer le gradient une fois pour toutes, à l’aide d’une formule mathématique, et résoudre le problème. Cela est permis par le fait que la fonction de coût a des bonnes propriétés (convexité), ce qui fait qu’il y a une unique solution optimale à notre problème, soit un unique minimum global.

Néanmoins, la descente de gradient est bien plus générale, en ce qu’elle peut s’appliquer à des modèles bien plus complexes pour lesquels calculer le gradient n’est pas simple, ou bien la fonction de coût n’est pas totalement convexe.

Un problème non-linéaire

Code

N = 100
P = 1


def make_sine_regression(key, n, p):
    key1, key2, key3 = random.split(key, 3)
    x = 2 * random.normal(key1, [n, p])
    w = random.normal(key2, [p])
    b = random.normal(key3)
    noise = 0.2 * random.normal(key3, [n])

    # actual data generation process
    y = jnp.sin(x @ w + b) + noise
    return x, y, w, b


x, y, w_true, b_true = make_sine_regression(PRNGKey(2), 100, 1)

fig, ax = plt.subplots(figsize=(13, 10))
plt.scatter(x, y)
plt.title("Problème de régression")
plt.xlabel("Feature")
plt.ylabel("Cible")
plt.show()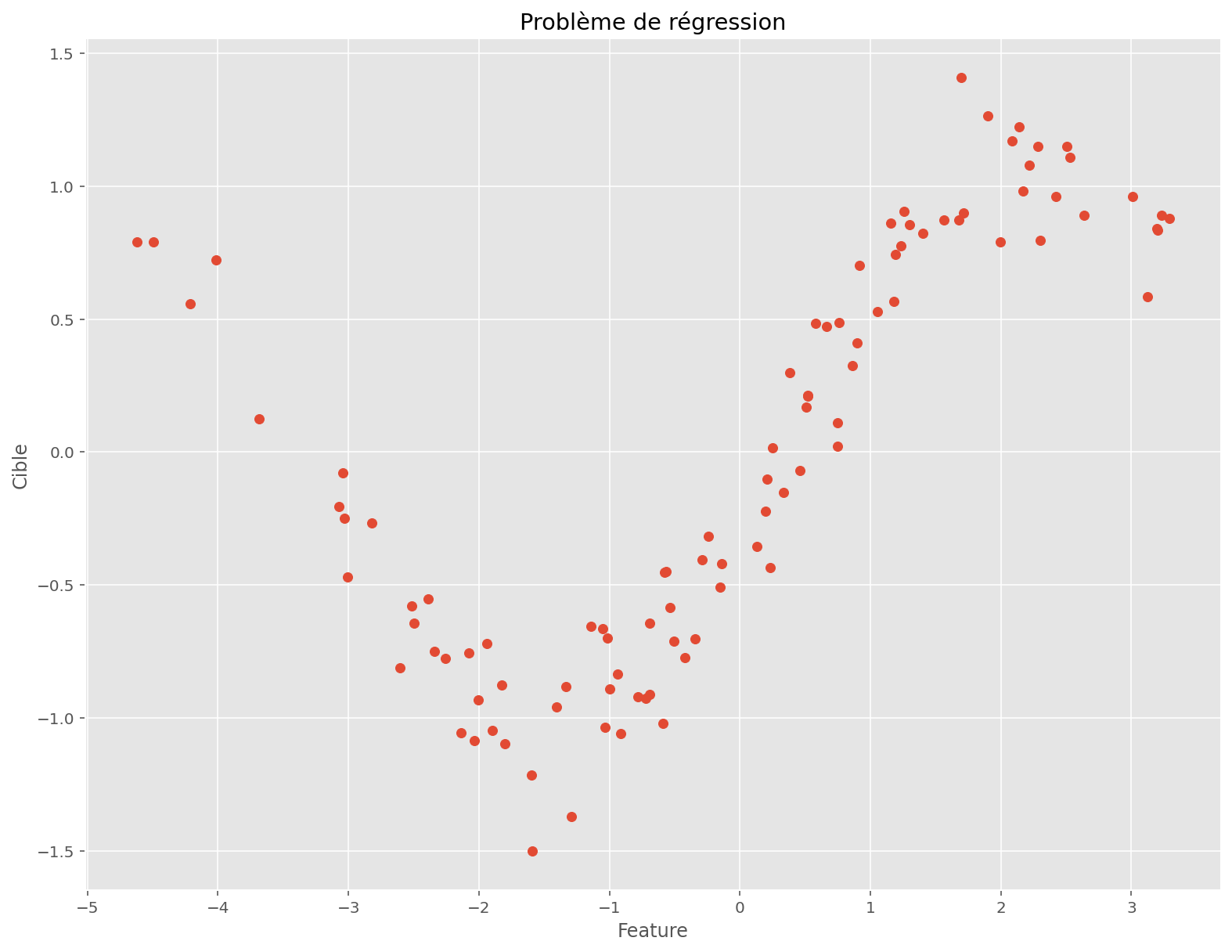

Régression linéaire

Code

n_train = 20
# initial_params = init_fn(PRNGKey(4), P)
initial_params = jnp.asarray([4.]), -1.5
params, memo = train(linear_loss, n_train, initial_params, x, y, lr=0.1)
plot_train(linear_apply_fn, initial_params, x, y, memo, params)

Coût initial: 56.88
Coût final: 0.36

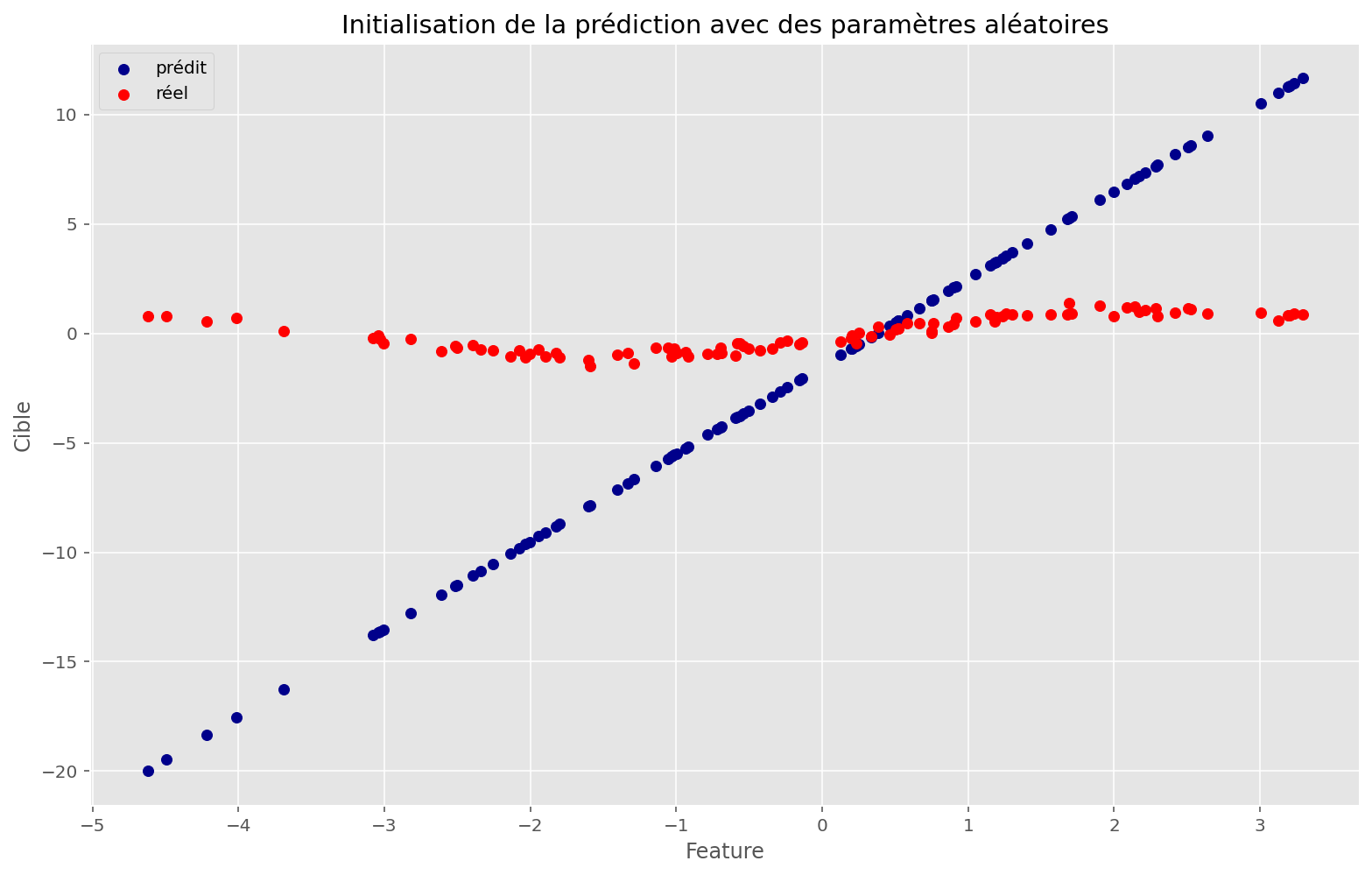
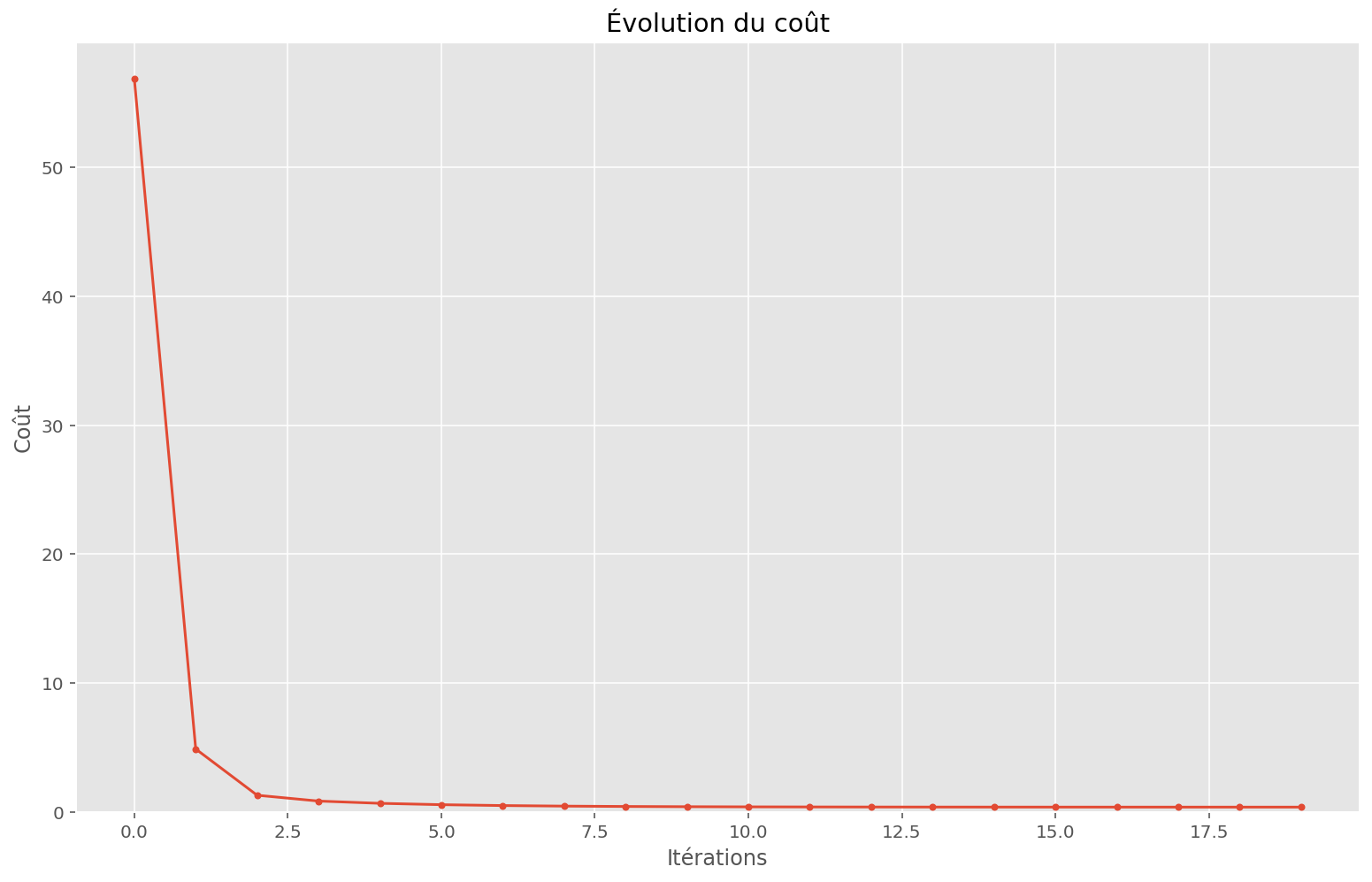
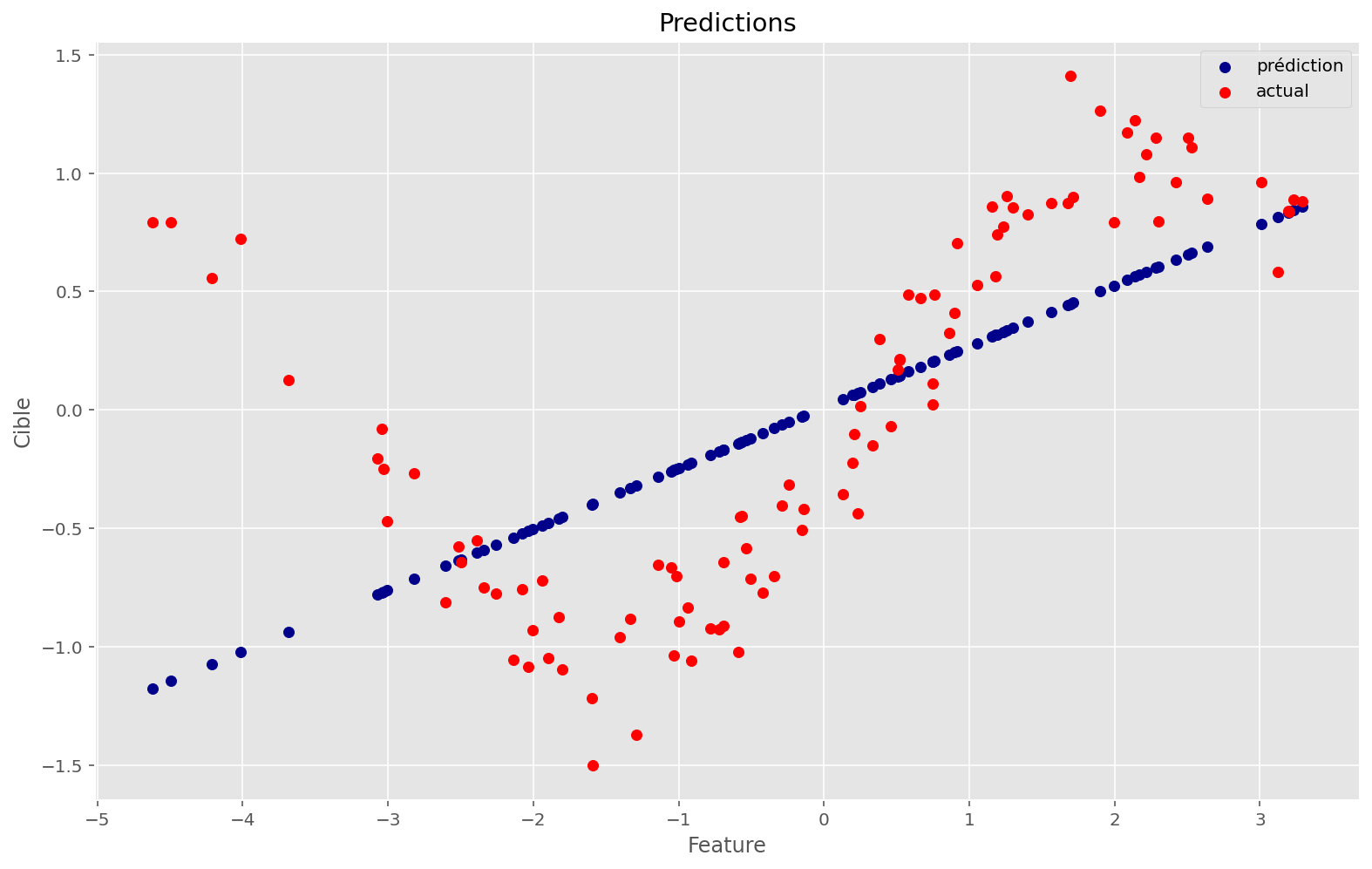
Comme on peut le voir, ce n’est pas une bonne prédiction. C’est expliqué par la nature de ce problème: il n’est pas linéaire.

Étrangement, la fonction de coût décroît très rapidement et on peut avoir l’impressions que les paramètres finaux permettent au modèle d’être performant. Pourtant, lorsque l’on affiche les prédictions, on voit bien que ce n’est pas satisfaisant.

Qu’est-ce que le modèle voit dans ces conditions?

Code

U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    partial(linear_loss, x=x, y=y)
)

fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, gradnorm, fig, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")
ax.set_zlabel("Coût")
plt.title("Coût en fonction des paramètres")

fig, ax = plt.subplots(figsize=(13, 10))
plot_quiver(U, V, gradx, grady, gradnorm, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")

plot_gradient_descent(memo[:, 1:3], ax=ax)
plt.title("Champ vectoriel du gradient\net algorithme de descente")
plt.show()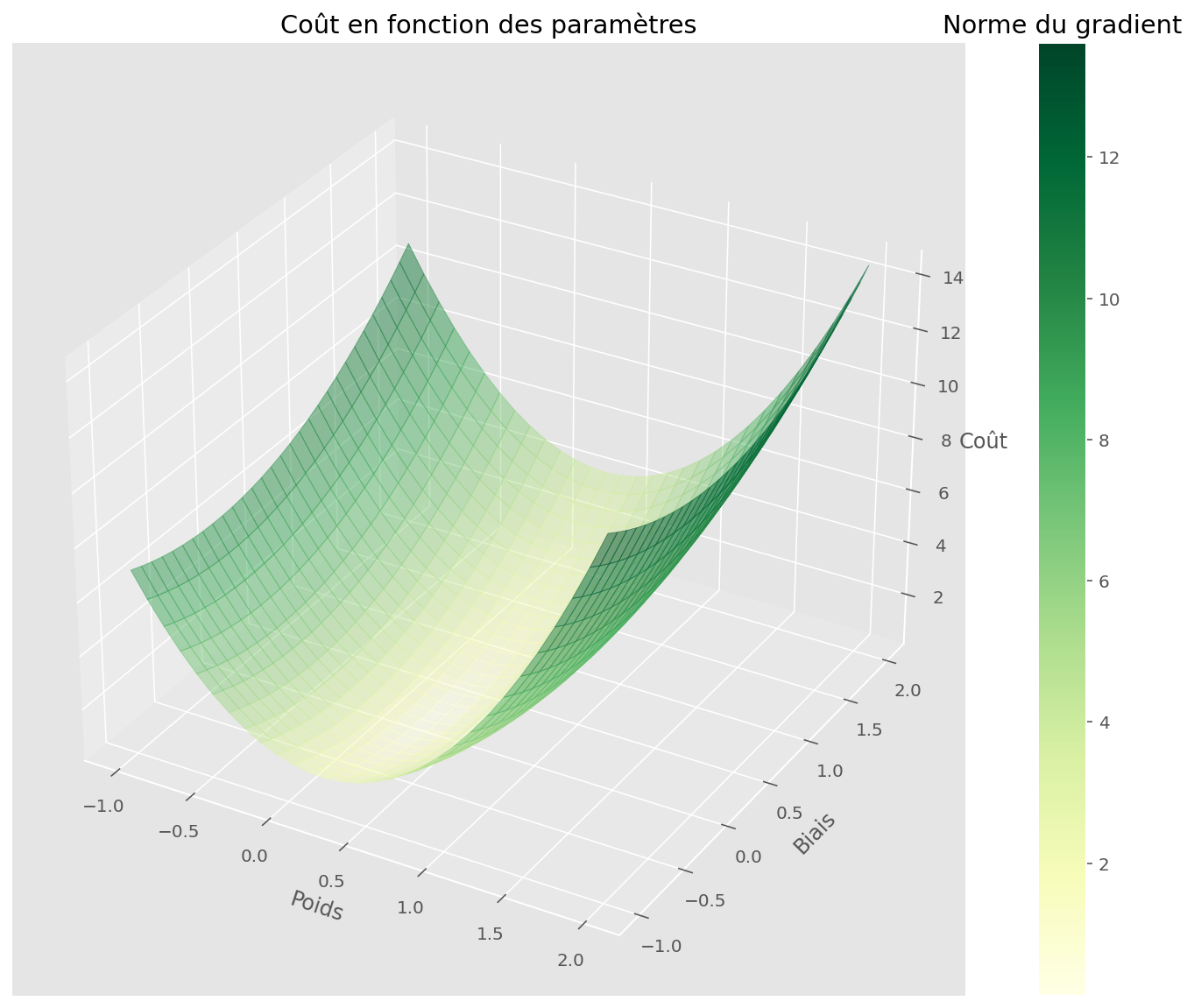

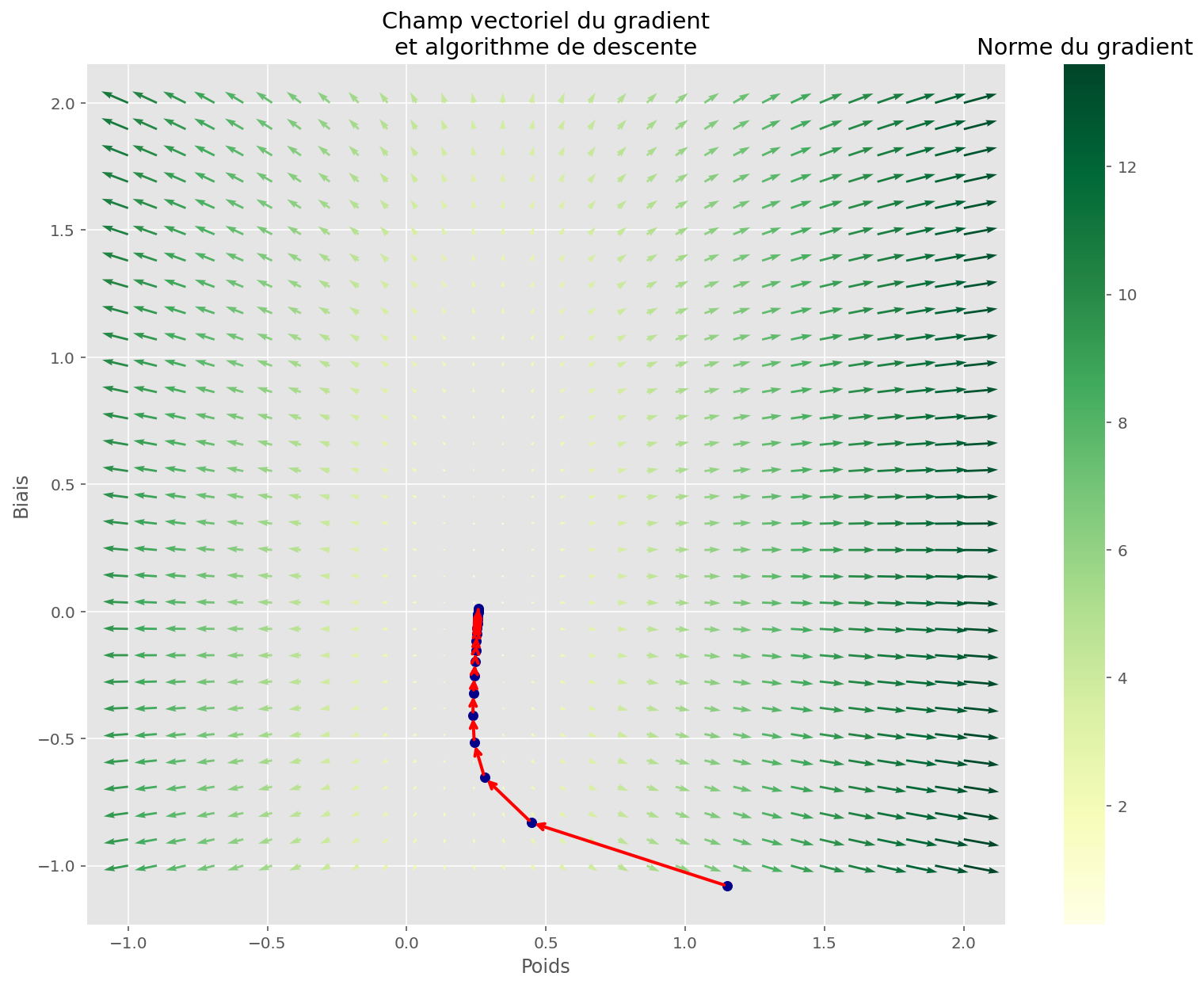
L’algorithme de descente a bien fonctionné, car il a bien trouvé un minimiseur de la fonction de coût.

Cela n’est pas satisfaisant car le processus de génération de données n’est pas linéaire, ce qui veut dire qu’on ne peut pas approximer la solution en traçant une droite.

Régression sinusoïdale

Une astuce consiste à appliquer une fonction sinus après la sortie de la fonction linéaire. Comme la donnée a été générée avec une fonction similaire, on sait que le modèle est capable d’une bonne approximation.

Code

def sin_apply_fn(params, x):
    w, b = params
    out = jnp.sin(x @ w + b)
    return out


sin_loss = partial(make_loss, sin_apply_fn)
grad_sin_loss = jit(grad(sin_loss))

initial_params = jnp.asarray([4.]), -2.

params, memo = train(sin_loss, n_train, initial_params, x, y, lr=0.2)

plot_train(sin_apply_fn, initial_params, x, y, memo, params)

Coût initial: 1.25
Coût final: 1.04

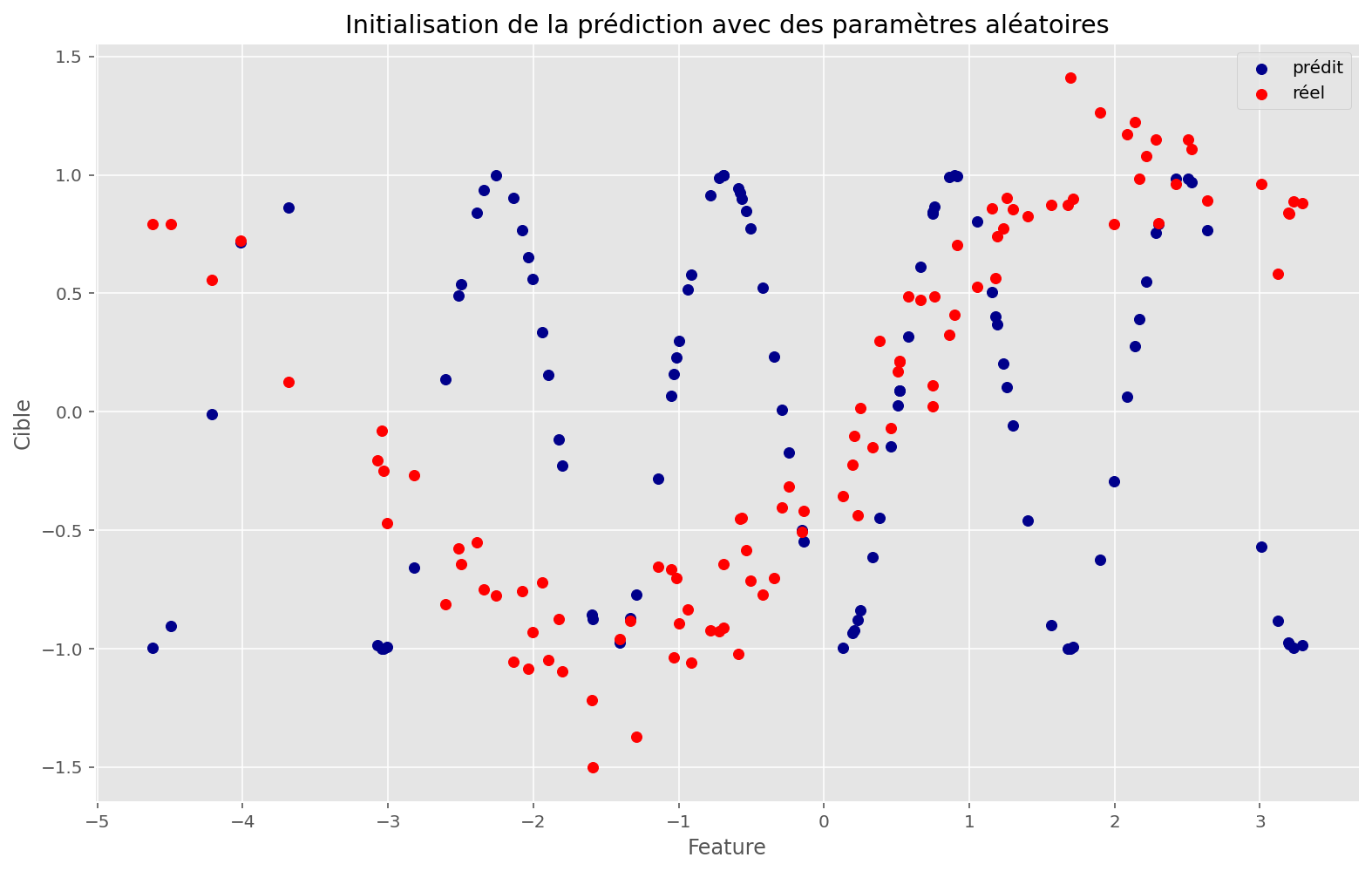
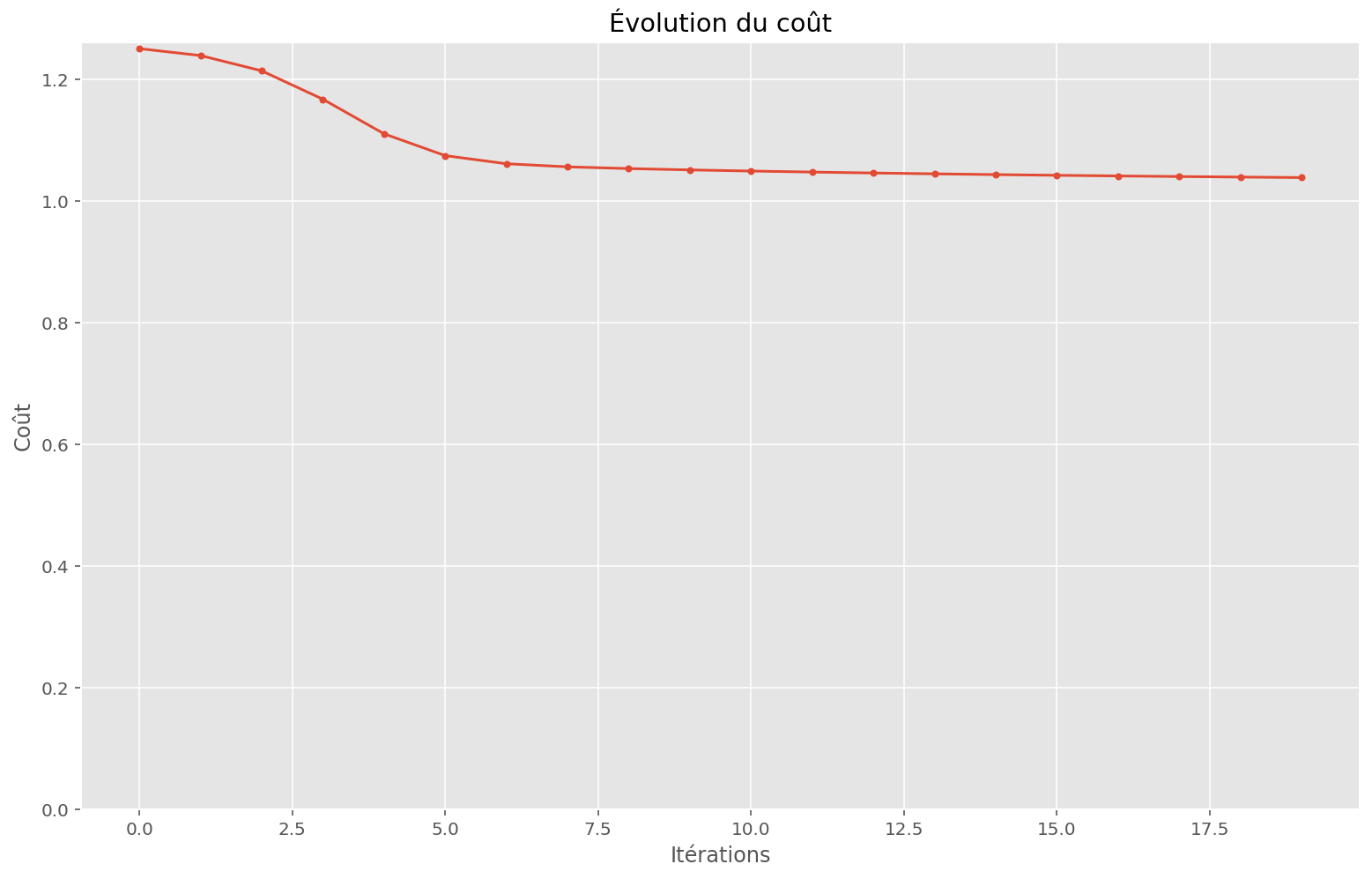
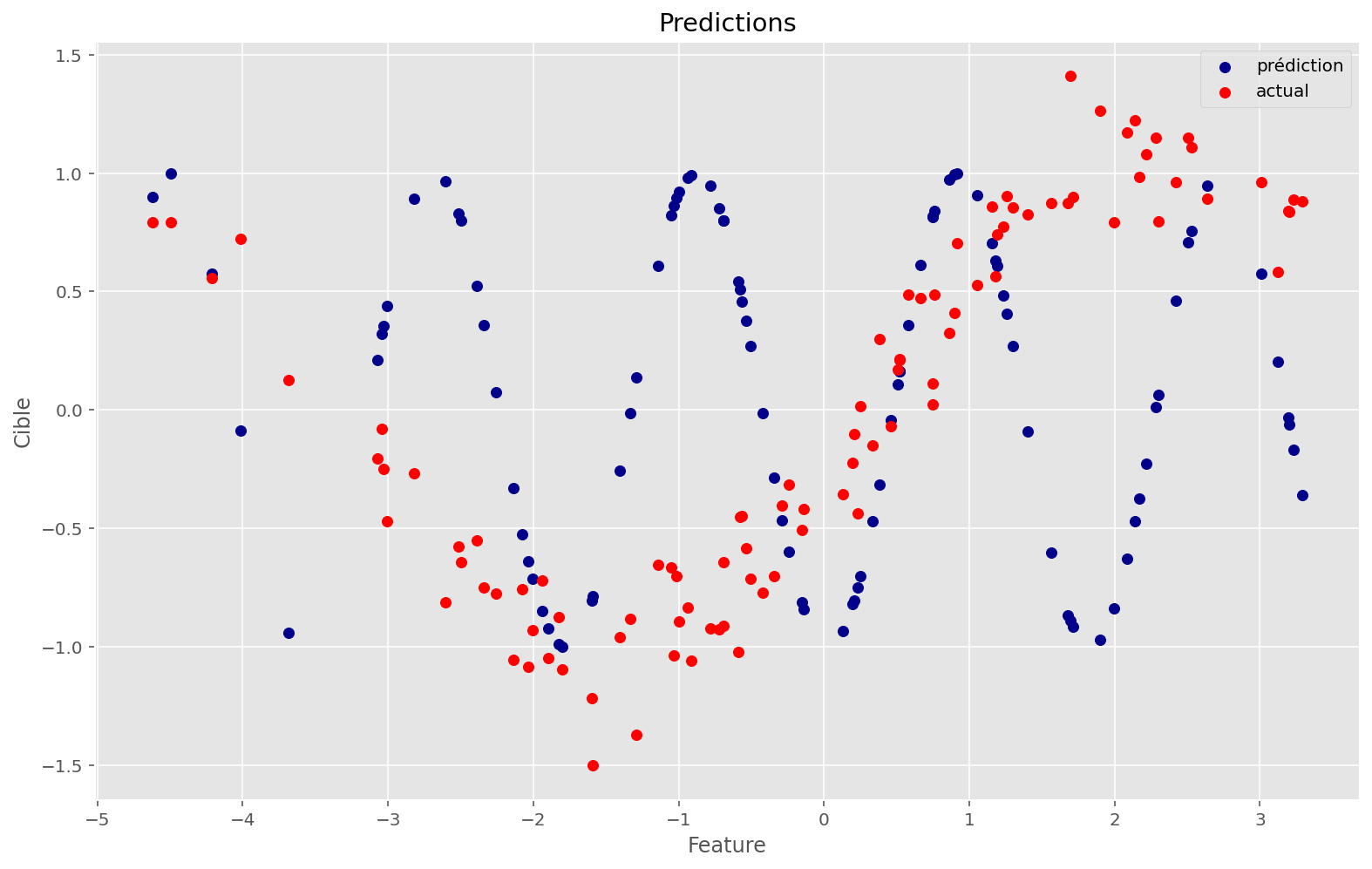
La fonction approximée ne fonctionne pas. À quoi ressemble l’espace de la fonction de coût ?

Code

U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    partial(sin_loss, x=x, y=y), xrange=(-4, 4), yrange=(-4, 0)
)

fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, gradnorm, fig, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")
ax.set_zlabel("Coût")
plt.title("Coût en fonction des paramètres")

fig, ax = plt.subplots(figsize=(13, 10))
plot_quiver(U, V, gradx, grady, gradnorm, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")

plot_gradient_descent(memo[:, 1:3], ax=ax)
plt.title("Champ vectoriel du gradient\net algorithme de descente")
plt.show()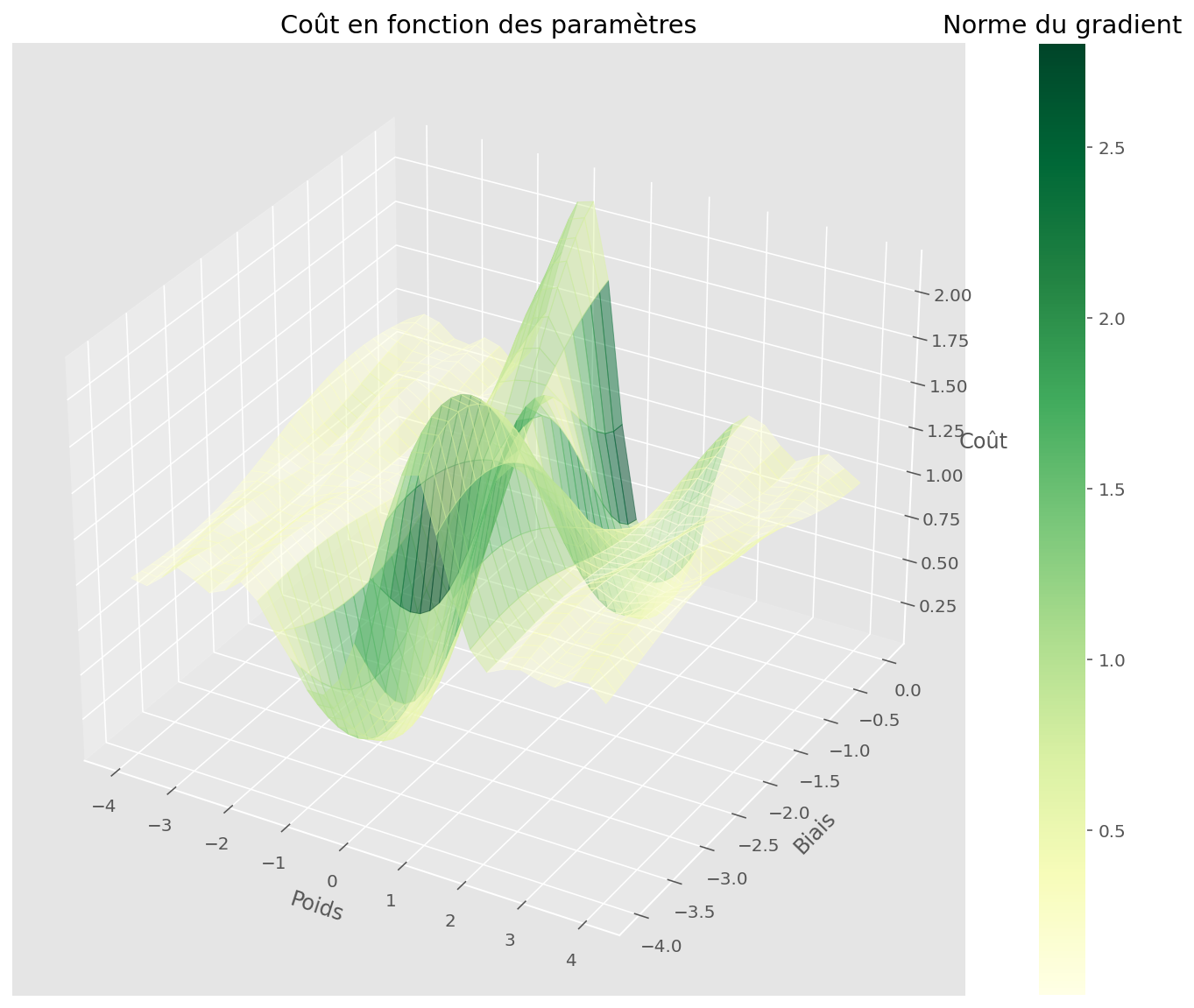

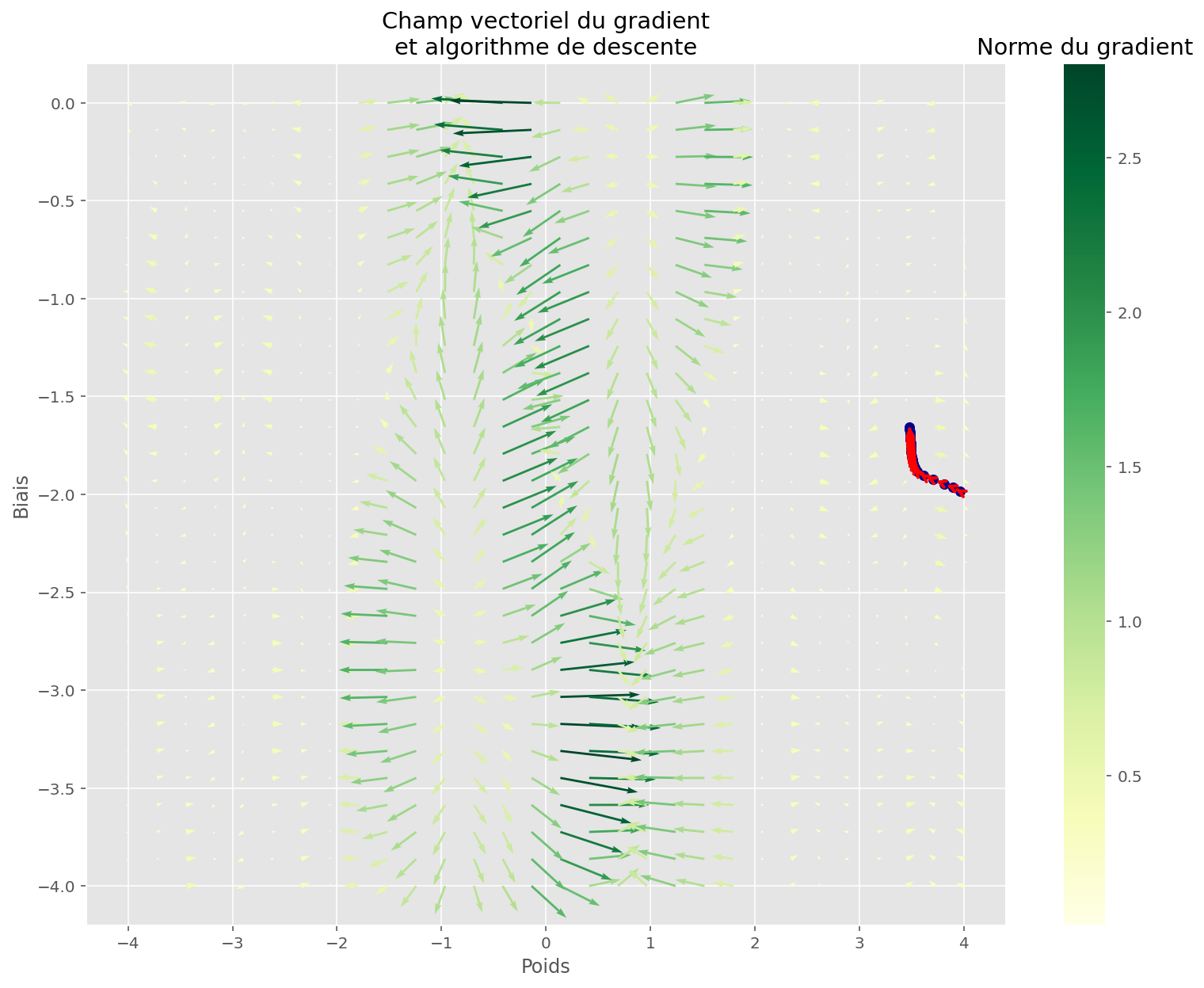
En examinant la descente, on voit que l’algorithme est resté bloqué dans un minimum local.

Pour résoudre ceci, on peut utiliser de l’inertie:

Code

params, memo = train_opt(partial(sin_loss, x=x, y=y), optimizers.momentum(.94, 0.87), 150, initial_params)
U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    partial(sin_loss, x=x, y=y), xrange=(-2, 4), yrange=(-3,3)
)
plot_train(sin_apply_fn, initial_params, x, y, params=params, memo=memo["loss"].reshape(-1, 1))

# fig = plt.figure(figsize=(15, 10))
# ax = fig.gca(projection="3d")
# plot_surface(U, V, Z, gradnorm, fig, ax)
# plt.xlabel("Poids")
# plt.ylabel("Biais")
# ax.set_zlabel("Coût")
# plt.title("Coût en fonction des paramètres")

fig, ax = plt.subplots(figsize=(13, 10))
plot_quiver(U, V, gradx, grady, gradnorm, ax)
plt.xlabel("Poids")
plt.ylabel("Biais")

memo_params = jnp.dstack(jax.tree_map(jnp.ravel, memo["params"]))[0]
plot_gradient_descent(memo_params, ax=ax, alpha=0.3)
plt.title("Champ vectoriel du gradient\net algorithme de descente avec inertie")
plt.show()

Coût initial: 1.25
Coût final: 0.03

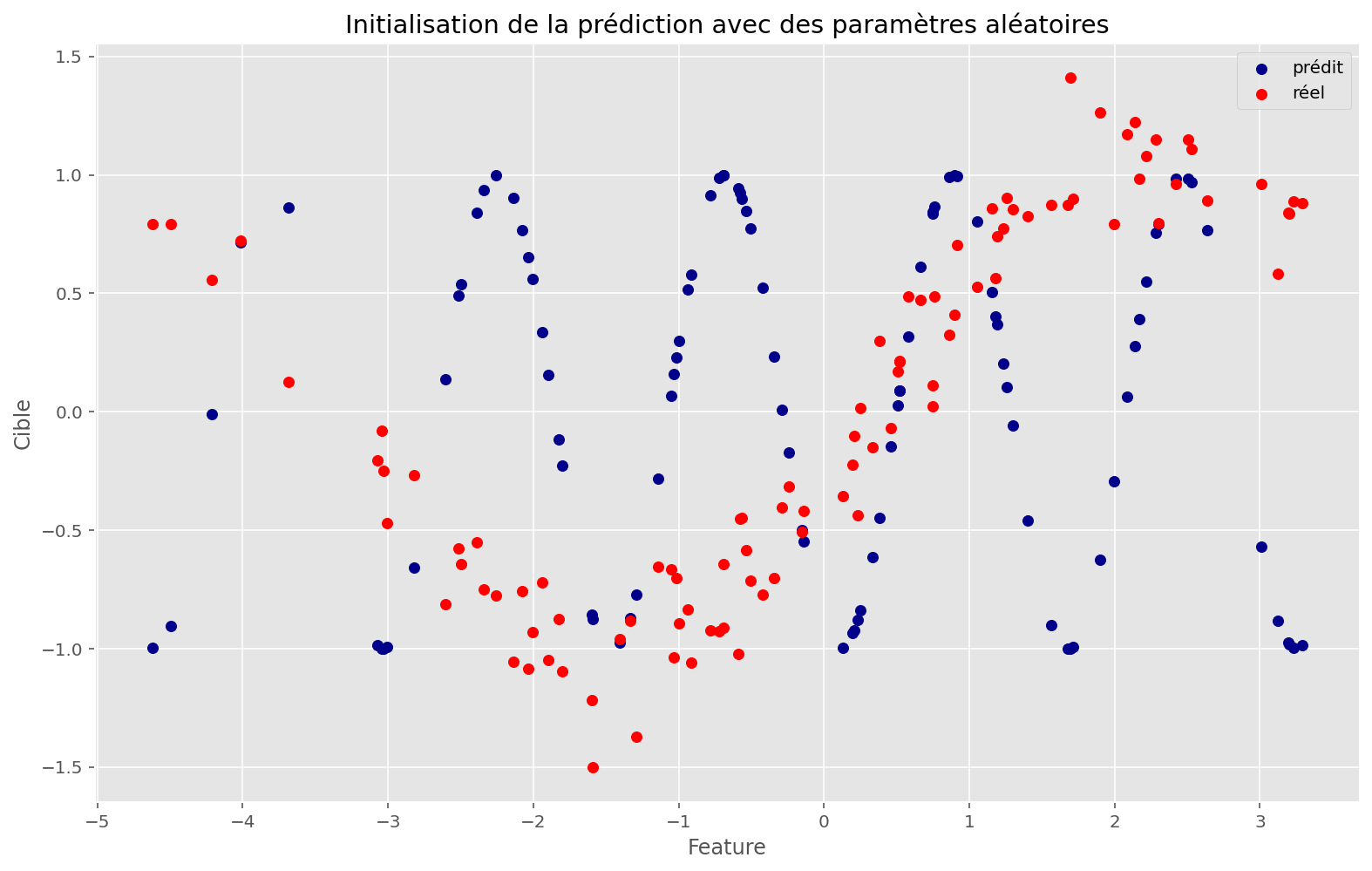
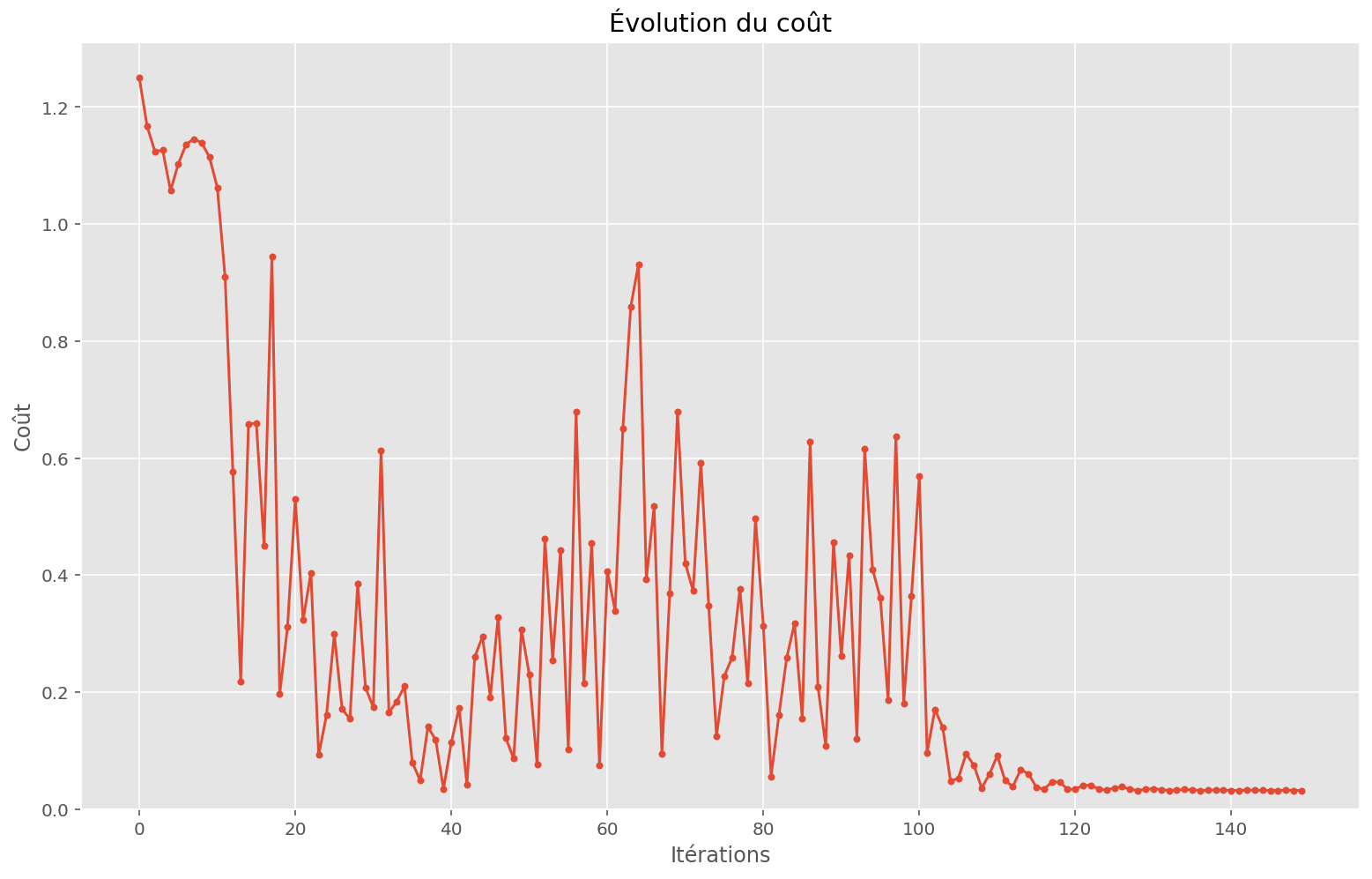
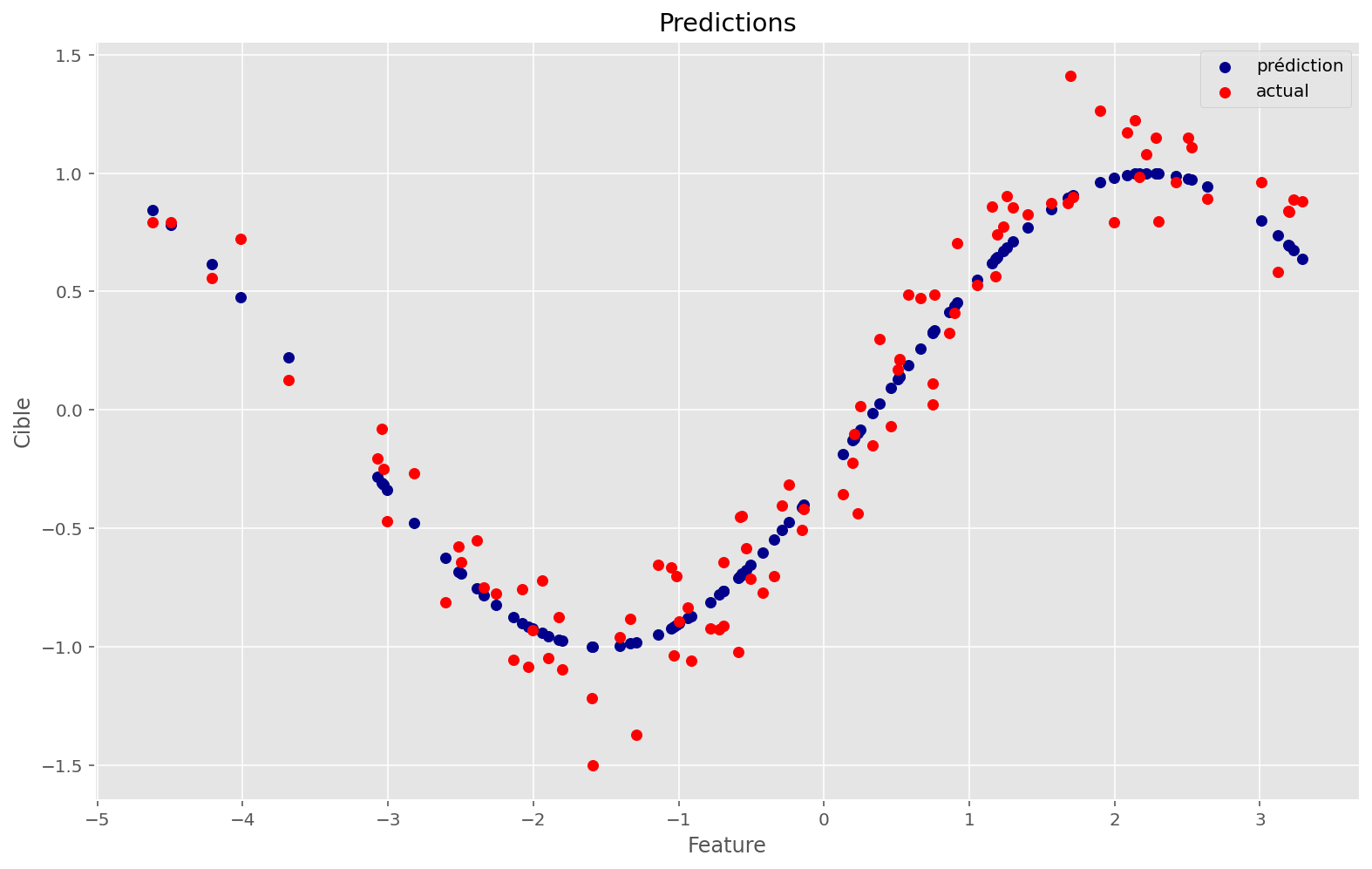
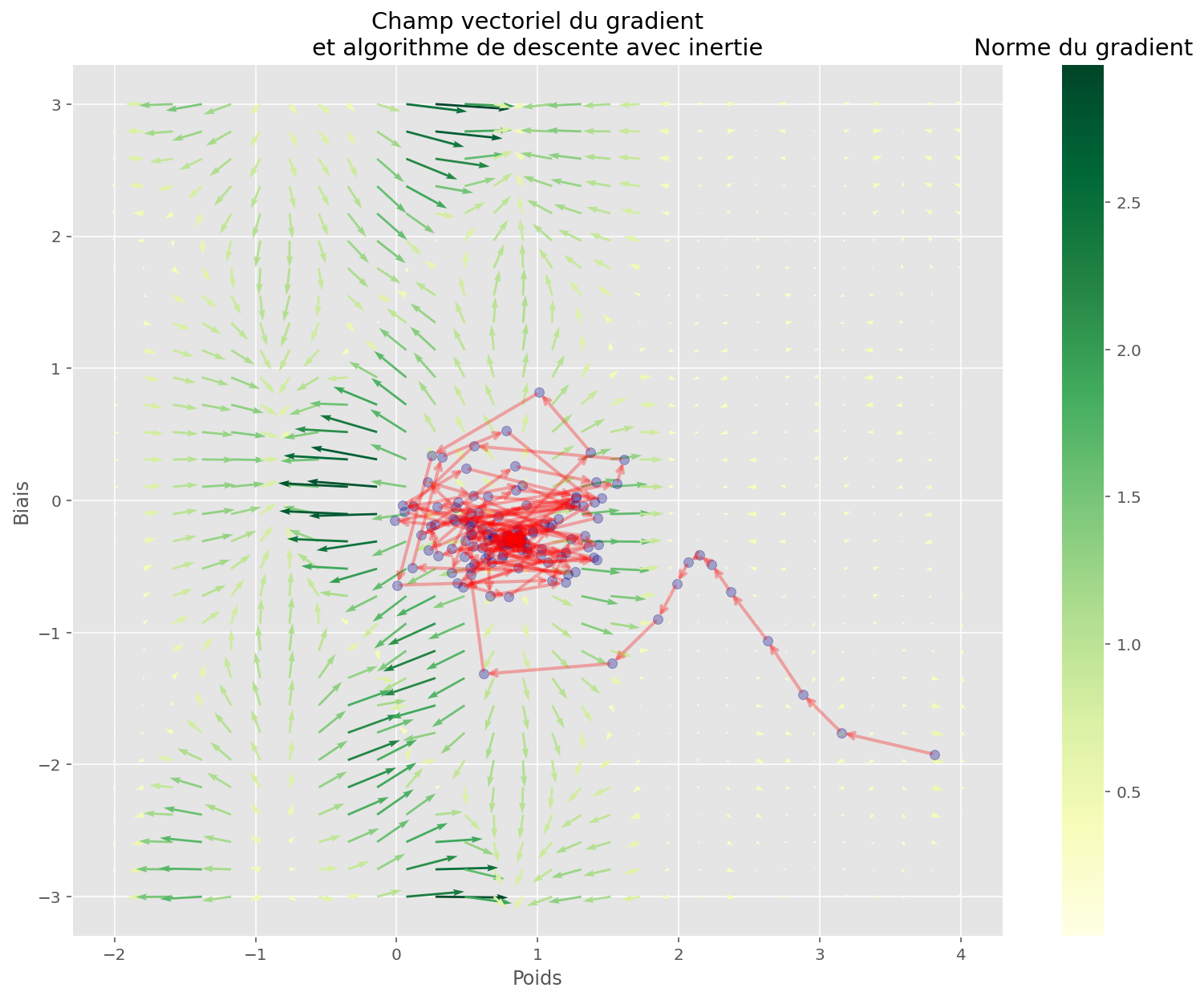
L’espace est plus complexe, mais la fonction a quand même réussi à trouver un bon minimum. Les conditions initiales ont sûrement joué.

Comme on peut le voir, la nouvelle fonction colle presque parfaitement aux données.

Un problème linéaire large

On peut se demander ce qu’il se passe lorsqu’on rajoute des dimensions.

Nous allons ici prendre un problème de type large: nous avons 40 dimensions (features), pour 150 observations et une cible à une dimension et une relation linéaire entre les features et la cible.

Pour rajouter de la difficulté, on va utiliser des features qui sont corrélées entre elles. Seulent 10 features apportent l’information initiale, et les 30 restantes ne sont qu’une répétition d’une autre feature mutipliée par un coefficient au hasard.

Reprenons notre modèle linéaire, car ici il n’y a pas de raison que la donnée oscille à la manière du sinus.

Code

N = 150
P = 40
rank = 10


def make_wide_regression(key, n, p, rank):
    assert rank <= p
    key1, key2, key3, key4, key5 = random.split(key, 5)
    x = random.normal(key1, [n, p])
    w = random.permutation(
        #         key2, jnp.hstack([random.normal(key2, [rank]), jnp.zeros([p - rank])])
        key2,
        random.normal(key5, [p])
        * jnp.hstack(
            [
                jnp.repeat(random.normal(key2, [rank]), p // rank),
                jnp.zeros([p % rank]),
            ]
        ),
    )
    b = random.normal(key3)
    noise = random.normal(key4, [n])

    # actual data generation process
    y = x @ w + b + noise
    return x, y, w, b


x, y, w_true, b_true = make_wide_regression(PRNGKey(2), N, P, rank)

n_train = 50
initial_params = init_fn(PRNGKey(10), P)
params, memo = train(
    linear_loss,
    n_train,
    initial_params,
    x,
    y,
)

w_found, b_found = params
# print(f"True parameters", np.asarray(w_true), b_true, sep="\n")
# print(f"Found parameters", np.asarray(w_found), b_found, sep="\n")
print(f"Final loss: {memo[-1, 0]:.2f}")
plt.plot(memo[:, 0])
plt.show()

Final loss: 0.75

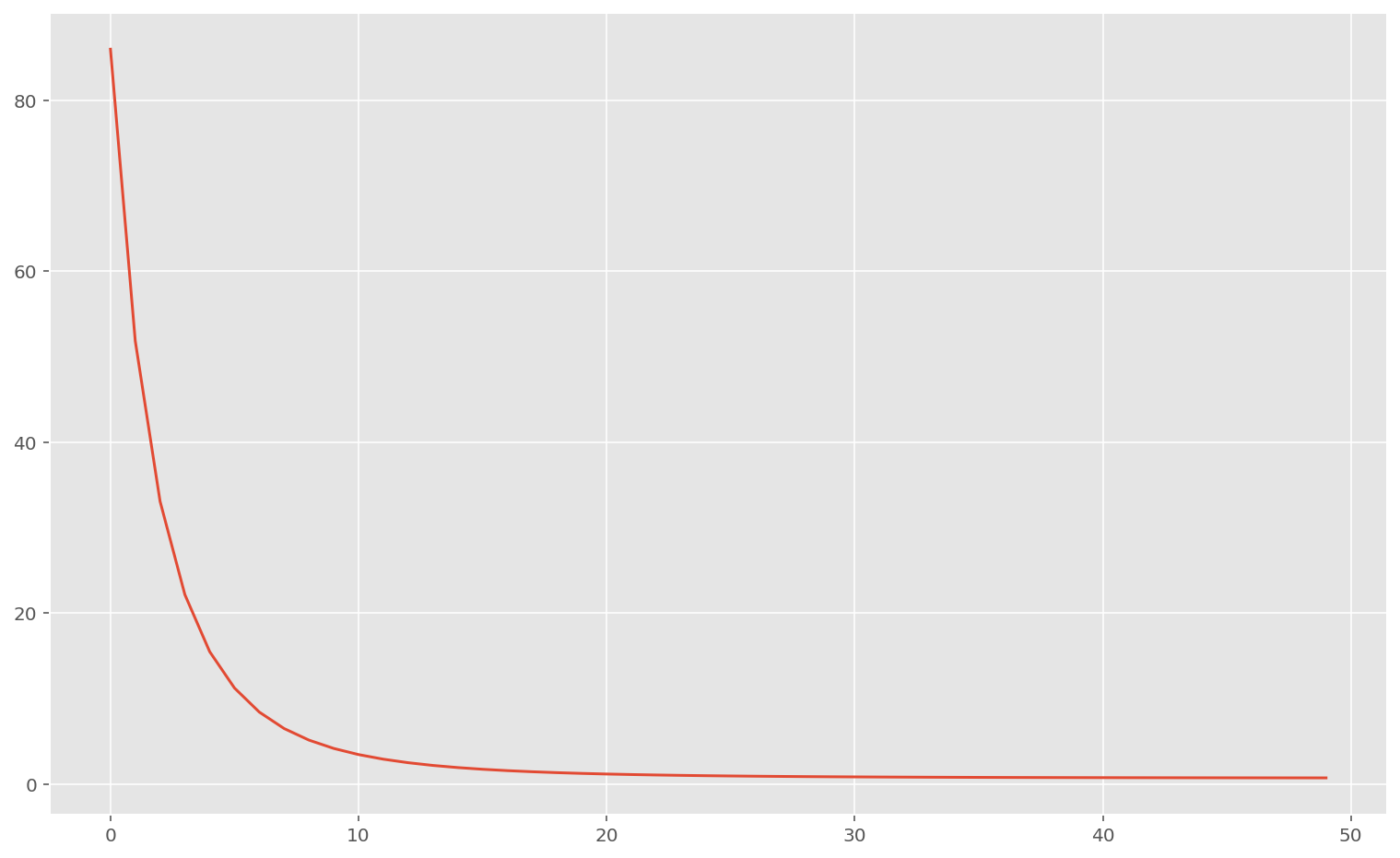
On a l’impression que le processus fonctionne bien : la fonction de coût décroit pour atteindre une valeur proche de zéro.

Néanmoins, nous allons voir que le modèle (linéaire) n’est pas capable de généraliser sur de nouvelles données.

Pour bien comprendre le phénomène, nous allons utiliser une technique de machine learning qui consiste à séparer notre jeu de données en deux :

• Un jeu de donnnées pour l’entraînement x_tr, y_tr
• Un jeu de données pour la validation x_te, y_te

On effectue une descente de gradient sur l’ensemble d’entraînement, puis on évalue la performance en calculant la fonction de coût sur l’ensemble de test :

Code

split = int(N // 3)
x_tr, x_te = x[:split], x[split:]
y_tr, y_te = y[:split], y[split:]
params, memo = train(linear_loss, n_train, initial_params, x_tr, y_tr)
print(f"Train loss: {memo[-1, 0]:.4f}")

print("Test loss:", linear_loss(params, x_te, y_te))

Train loss: 0.7077
Test loss: 12.389101

Le coût est presque 20 fois plus élevé sur le jeu de données de test !

Cela indique un phénomène bien identifié dans le machine learning: le sur-apprentissage (overfitting). Pour réduire ce phénomène, on peut par exemple modifier la fonction de coût utilisée pour entraîner notre modèle en pénalisant la complexité du modèle : c’est ce qu’on appelle la régularisation.

Régularisation Ridge

Cela peut se faire en ajoutant la norme (au carré) des paramètres à la fonction de coût, multipliée par un coefficient qui mesure l’intensité de la pénalisation : c’est un hyperparamètre, qui n’est pas appris par le modèle mais sélectionné manuellement par la personne qui expérimente.

Ensuite, il ne faut pas oublier de mesurer la performance avec la fonction de coût originale, sur l’ensemble de test. Ce processus nous sert de métrique.

Code

@partial(jit, static_argnums=0)
def make_ridge_loss(apply_fn, params, x, y, reg=1.0):
    ls = jnp.sum((apply_fn(params, x) - y) ** 2)
    pen = jnp.linalg.norm(jnp.hstack(params), ord=2) ** 2
    return (ls + reg * pen) / y.shape[0]


linear_ridge_loss = partial(make_ridge_loss, linear_apply_fn, reg=5.0)

params, memo = train(
    linear_ridge_loss,
    n_train,
    initial_params,
    x_tr,
    y_tr,
)

plt.plot(memo[:, 0])

print(f"Train loss:", linear_loss(params, x_tr, y_tr))
print("Test loss:", linear_loss(params, x_te, y_te))

w_found, b_found = params
# print(f"True parameters", np.asarray(w_true), b_true, sep="\n")
# print(f"Found parameters", np.asarray(w_found), b_found, sep="\n")

Train loss: 1.2346672
Test loss: 8.390494

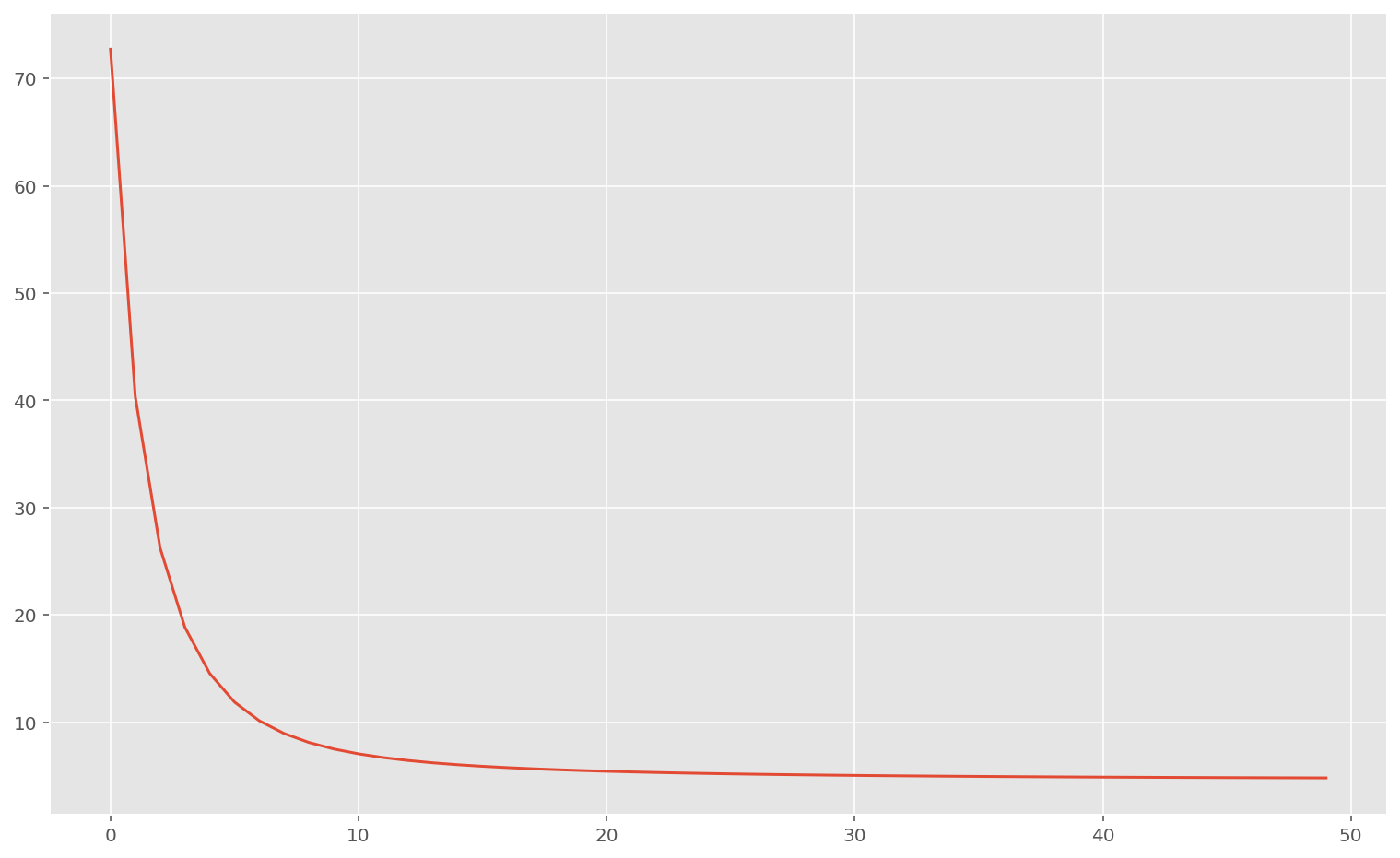
On peut voir que l’erreur a diminué sur l’ensemble de test, ce qui signifie que la technique de régularisation a bien fonctionné : on a un modèle plus performant.

Néanmoins, on a dû sélectionner à la main deux hyper-paramètres : celui contrôlant la régularisation d’une part, et le taux d’apprentissage d’autre part.

Comment peut-on sélectionner les meilleurs hyperparamètres ?

Meta-apprentissage

A rebours des techniques classiques gradient-free comme la grid search, nous allons ici employer une fois encore le gradient. Cette fois-ci, ce n’est pas le gradient de la fonction de coût par rapport aux paramètres que nous souhaitons apprendre que nous allons évaluer, mais plutôt le gradient de notre métrique de performance sur l’ensemble de test, par rapport à nos hyperparamètres :

• Le taux d’apprentissage
• Le coefficient de régularisation

Nous avons donc affaire à des gradients imbriqués.

Code

def loss_graddec(graddesc_params):
    reg, lr = graddesc_params
    loss = partial(make_ridge_loss, linear_apply_fn, reg=reg)
    params, memo = train_opt(
        partial(loss, x=x_tr, y=y_tr), optimizers.adagrad(lr), n_train, initial_params
    )
    test_loss = linear_loss(params, x_te, y_te)
    return test_loss


best_meta, memo_meta = train_opt(
    loss_graddec, optimizers.momentum(step_size=0.2, mass=0.8), 50, (1.0, 1.0)
)

plt.plot(memo_meta["loss"])
plt.ylim(0)

print("Loss finale:", memo_meta["loss"][-1])
print("Meilleur coefficient de régularisation:", best_meta[0])
print("Meilleur taux d'apprentissage:", best_meta[1])

Loss finale:  3.2621257
Meilleur coefficient de régularisation: 0.76270264
Meilleur taux d'apprentissage: 10.747642

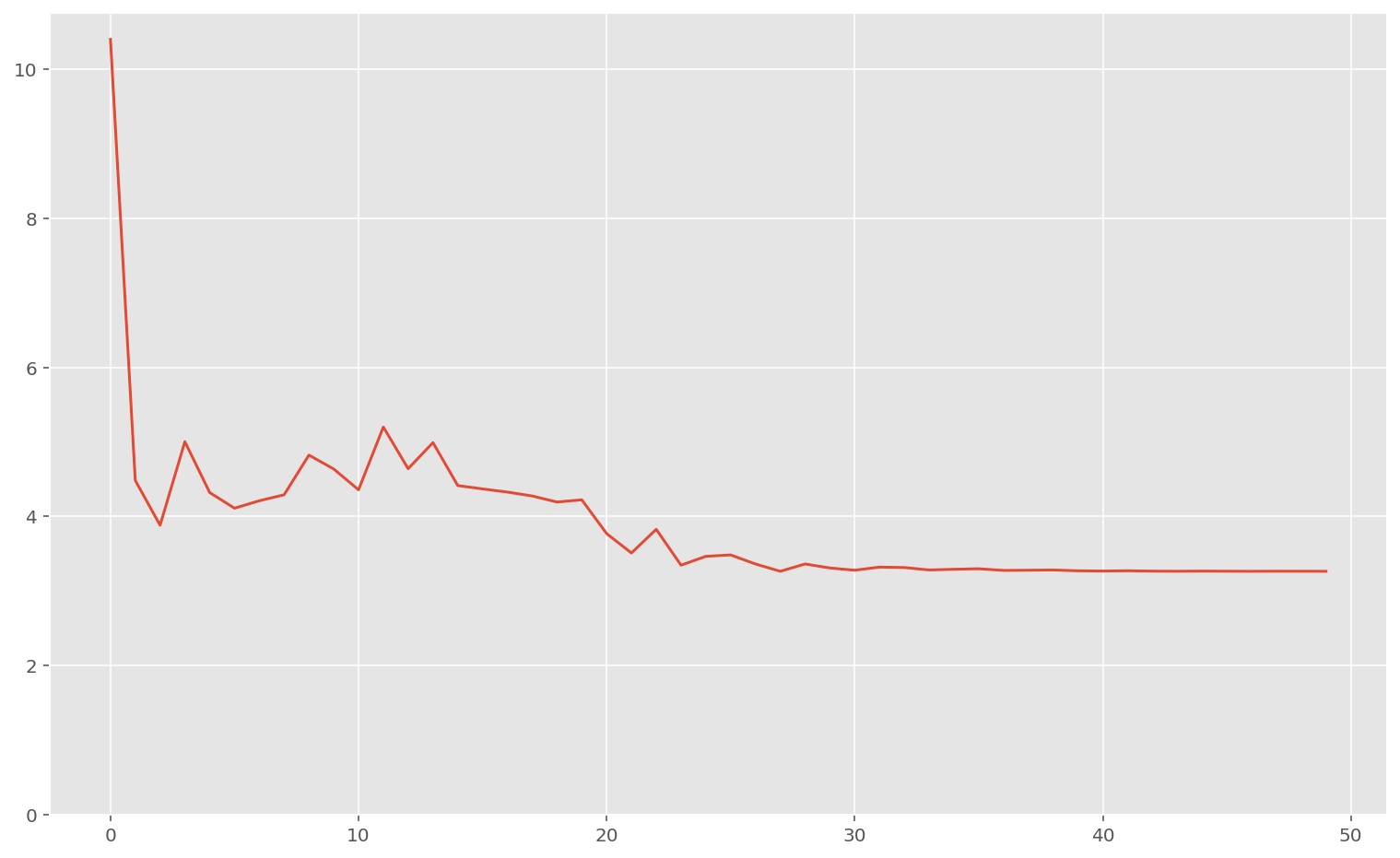
Code

jitted_mgf = jit(make_gradient_field, static_argnums=(0, 3, 4))

xrange = memo_meta["params"][0].min(), memo_meta["params"][0].max()
yrange = memo_meta["params"][1].min(), memo_meta["params"][1].max()

U, V, Z, pairs, gradvals, gradx, grady, gradnorm = jitted_mgf(
    loss_graddec,
    xrange,
    yrange,
    30,
    (2,),
)

CMAP = plt.cm.YlGn
fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, jnp.log1p(gradnorm), fig, ax, cmap=CMAP)
plt.xlabel("Coefficient de régularisation")
plt.ylabel("Taux d'apprentissage")
ax.set_zlabel("Coût")
plt.title("Coût en fonction des paramètres")

fig, ax = plt.subplots(figsize=(13, 10))
plot_quiver(U, V, gradx, grady, gradnorm, ax, cmap=CMAP)
plt.xlabel("Coefficient de régularisation")
plt.ylabel("Taux d'apprentissage")

memo_params = jnp.dstack(jax.tree_map(jnp.ravel, memo_meta["params"]))[0]
plot_gradient_descent(memo_params, ax=ax)
plt.title("Champ vectoriel du gradient\net algorithme de descente")
plt.show()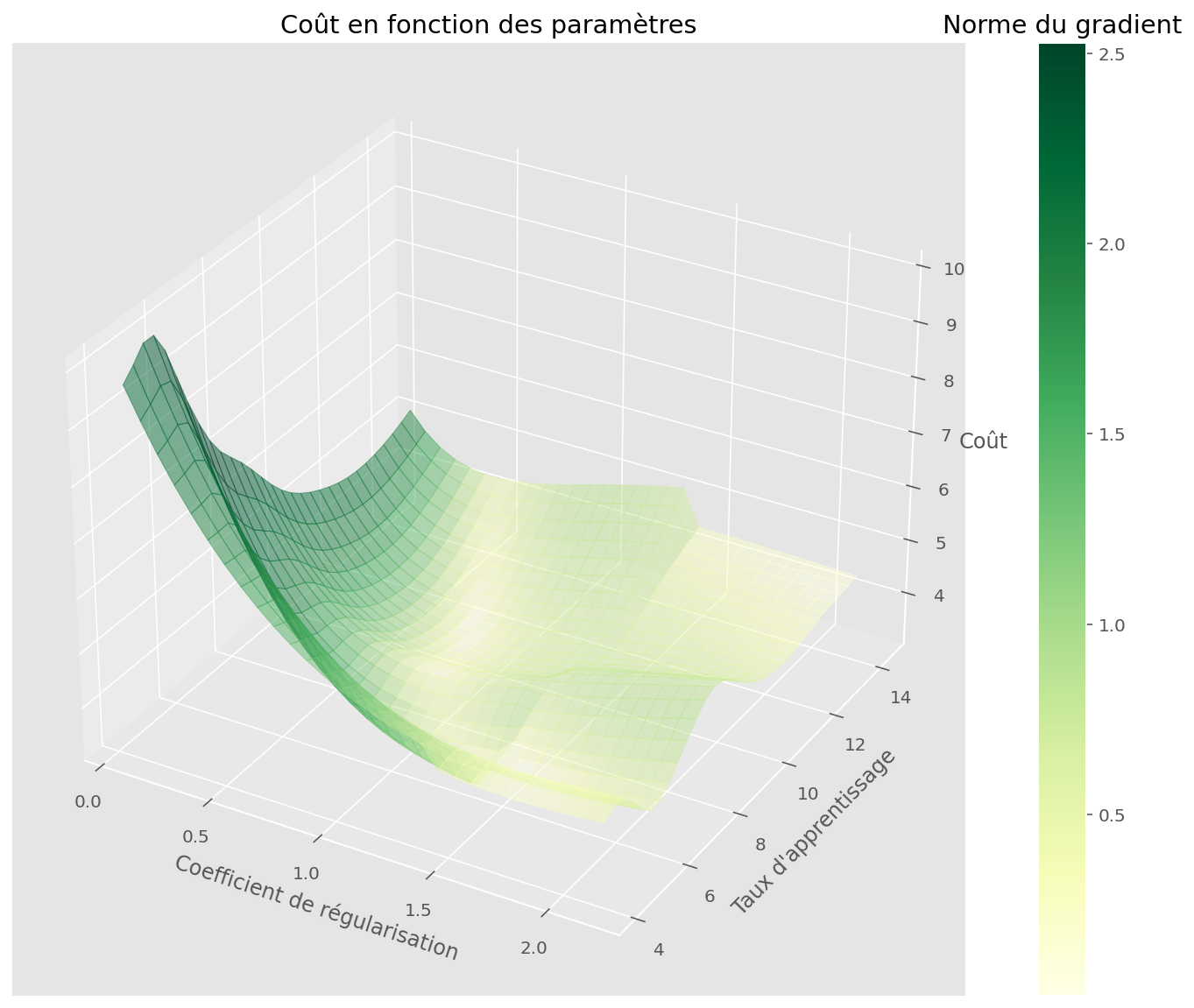

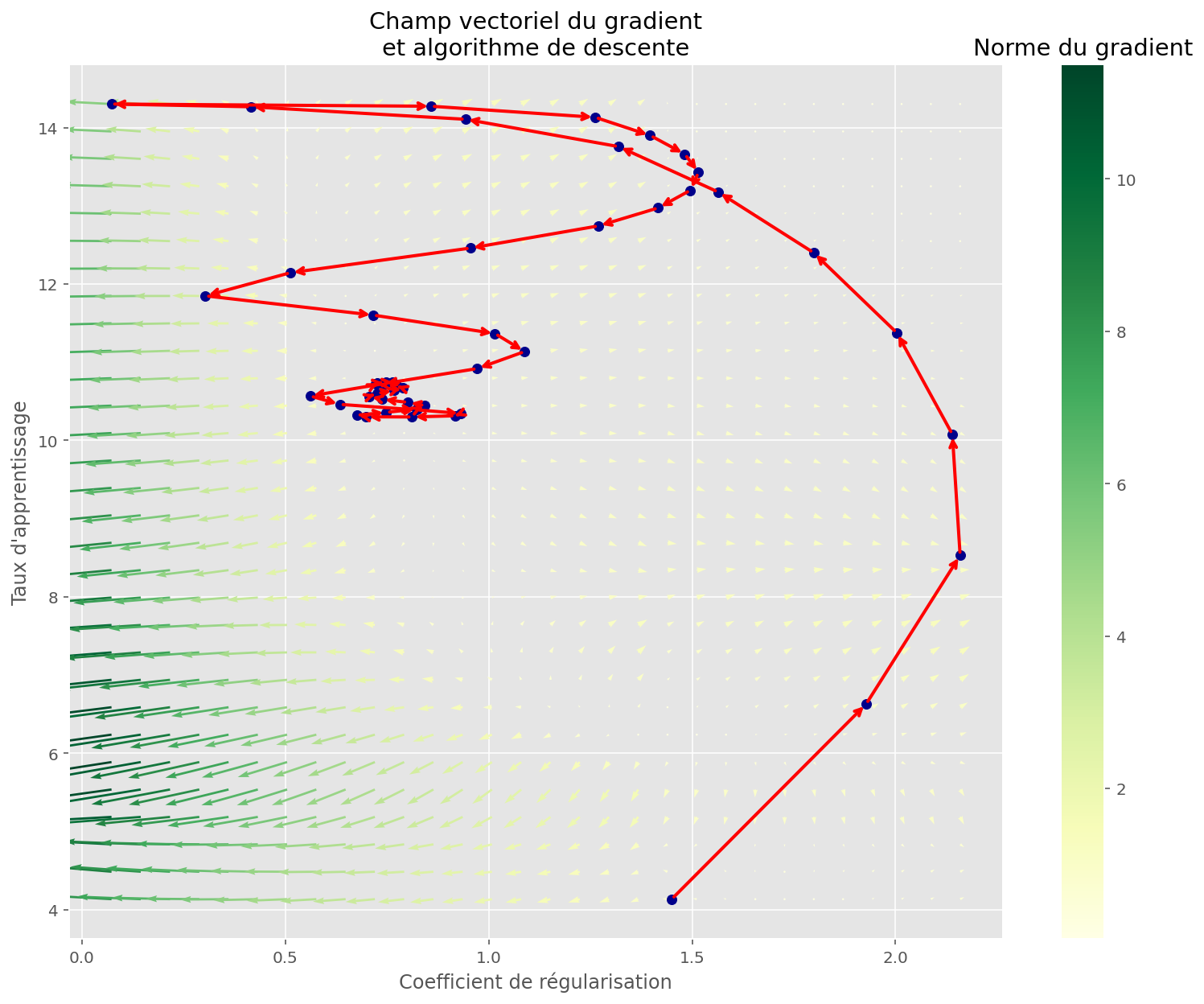
En prenant les meilleurs paramètres, et en appliquant la descente du gradient originale, on retrouve sans surprise la même valeur de coût :

Code

reg, lr = best_meta
loss = partial(make_ridge_loss, linear_apply_fn, reg=reg)
params, memo = train_opt(
    partial(loss, x=x_tr, y=y_tr), optimizers.adagrad(lr), n_train, initial_params
)

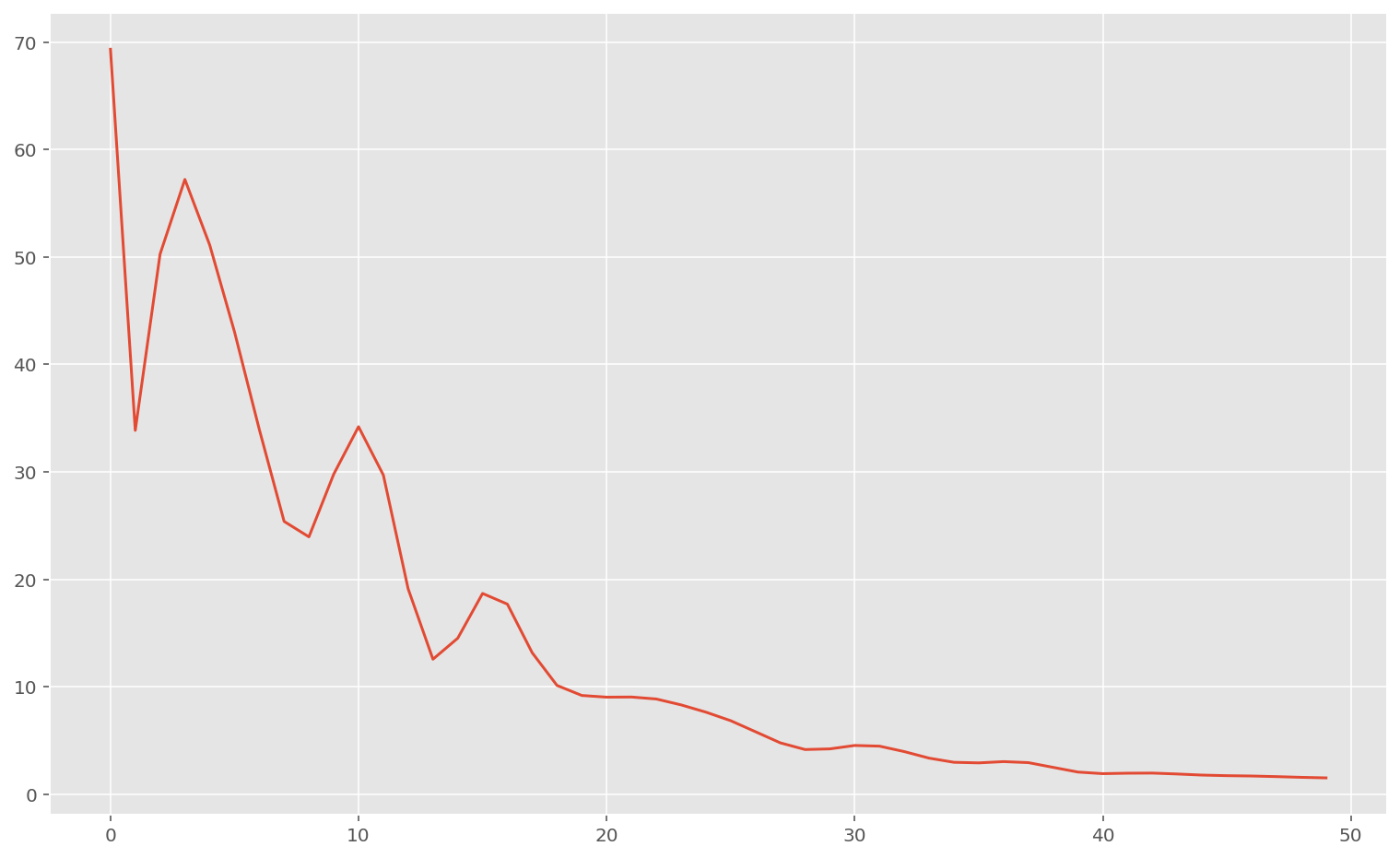
plt.plot(memo["loss"])

print(f"Train loss:", linear_loss(params, x_tr, y_tr))
print("Test loss:", linear_loss(params, x_te, y_te))

w_found, b_found = params
# print(f"True parameters", np.asarray(w_true), b_true, sep="\n")
# print(f"Found parameters", np.asarray(w_found), b_found, sep="\n")

Train loss: 0.65201813
Test loss: 3.2627606

Réseau de neurones

Pour finir, nous allons essayer avec un petit réseau de neurones à une couche (non-profond donc).

Nous allons prendre 10 neurones, et une activation [RELU](https://fr.wikipedia.org/wiki/Redresseur_(r%C3%A9seaux_neuronaux).

Code

from jax.experimental import stax
from jax.experimental.stax import Dense, Dropout, Relu

nn_init_fn, nn_apply_fn = stax.serial(Dense(10), Relu, Dense(1))

out_shape, net_params = nn_init_fn(PRNGKey(20), x.shape[1:])

stax_linear_loss = partial(make_loss, nn_apply_fn)
final_params, memo = train_opt(
    partial(stax_linear_loss, x=x_tr, y=y_tr.reshape(-1, 1)),
    optimizers.adagrad(0.6),
    100,
    net_params,
)
print("Train loss", stax_linear_loss(final_params, x_tr, y_tr.reshape(-1, 1)))
print("Test loss", stax_linear_loss(final_params, x_te, y_te.reshape(-1, 1)))

plt.plot(memo["loss"])
plt.show()

Train loss 0.00030381413
Test loss 32.594643

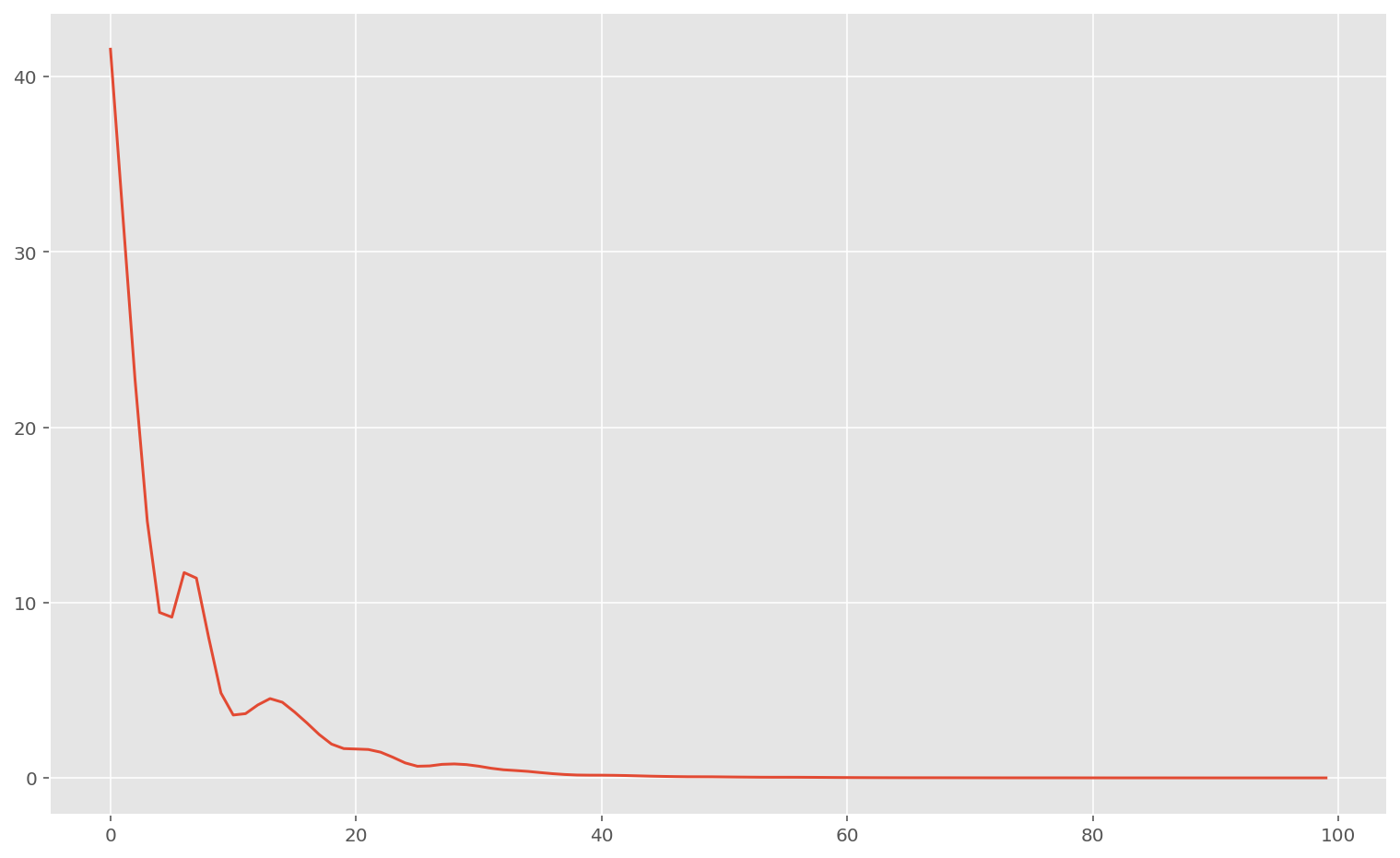
Comme on peut le voir, la performance est terrible. Ce n’est pas étonnant: un réseau de neurones n’est pas adapté à ce problème tabulaire, et overfit beaucoup.

Dropout

Ici on régularise les réseaux de neurons avec la technique du dropout.

Code

# on est obligés de ré-implémenter la fonction d'entraînement
# à cause de l'aléatoire dans le dropout

# just-in-time compilation, ignore function argument
# @partial(jit, static_argnums=0)
def make_rng_loss(apply_fn, params, x, y, rng):
    return jnp.mean((apply_fn(params, x, rng=rng) - y) ** 2)


@partial(jit, static_argnums=(0, 1, 2))
def train_dropout(loss_fn_xy, opt_triple, size, initial_params):
    opt_init, opt_update, get_params = opt_triple
    init_opt_state = opt_init(initial_params)

    def step(step, opt_state):
        loss, grads = jax.value_and_grad(partial(loss_fn_xy, rng=PRNGKey(step)))(
            get_params(opt_state)
        )
        opt_state = opt_update(step, grads, opt_state)
        return loss, opt_state

    def scan_fn(opt_state, i):
        loss, opt_state = step(i, opt_state)
        return opt_state, {"loss": loss, "params": get_params(opt_state)}

    opt_state, losses = jax.lax.scan(scan_fn, init_opt_state, jnp.arange(size))
    return get_params(opt_state), losses


n_neurons = 15

dropout = 0.3
nn_init_fn, nn_apply_fn = stax.serial(
    Dense(n_neurons),
    Dropout(dropout, mode="train"),
    Relu,
    Dense(n_neurons),
    Dropout(dropout, mode="train"),
    Relu,
    Dense(n_neurons),
    Dropout(dropout, mode="train"),
    Relu,
    Dense(1),
)
nn_init_fn_2, nn_apply_fn_2 = stax.serial(
    Dense(n_neurons),
    Dropout(dropout, mode="test"),
    Relu,
    Dense(n_neurons),
    Dropout(dropout, mode="test"),
    Relu,
    Dense(n_neurons),
    Dropout(dropout, mode="test"),
    Relu,
    Dense(1),
)

out_shape, net_params = nn_init_fn(PRNGKey(20), x.shape[1:])

stax_rng_linear_loss = partial(make_rng_loss, nn_apply_fn)

final_params, memo = train_dropout(
    partial(stax_rng_linear_loss, x=x_tr, y=y_tr.reshape(-1, 1)),
    optimizers.momentum(0.002, 0.7),
    1000,
    net_params,
)

print(
    "Train loss: ",
    make_rng_loss(nn_apply_fn_2, final_params, x_tr, y_tr.reshape(-1, 1), PRNGKey(0)),
)
print(
    "Test loss: ",
    make_rng_loss(nn_apply_fn_2, final_params, x_te, y_te.reshape(-1, 1), PRNGKey(0)),
)

plt.plot(memo["loss"])
plt.show()

Train loss:  36.658325
Test loss:  46.8016

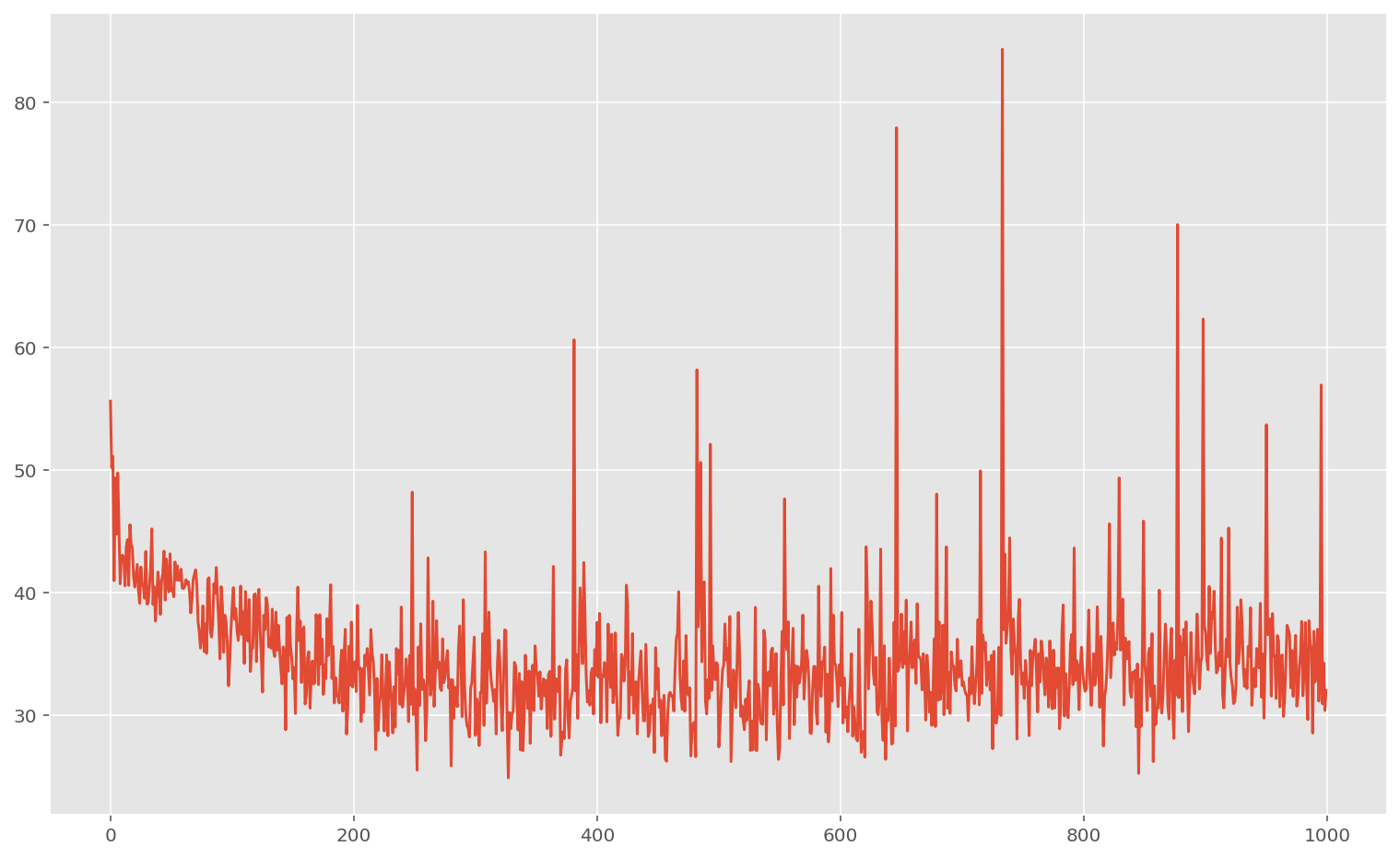
On voit que dans ce cas, le réseau n’overfit plus car il a quasiment le même score sur le jeu de données d’entraînement et le jeu de validation. Néanmoins, la performance est terrible sur les deux.

On peu donc conclure que les réseaux de neurones à architecture simple comme ceux-cis ne sont pas adaptés à ce genre de problème.

Conclusion

On a vu la puissance de la descente de gradient dans plusieurs cas que l’on pourrait qualifier de simple en terme de temps de calcul. En effet, on n’a eu ici juste eu besoin d’un processeur (CPU) et non de carte graphique (GPU) pour entraîner tous les modèles.

Pour résoudre des problèmes plus complexes et moins pédagogiques, on a besoin d’architecture beaucoup plus profondes et d’une grosse puissance de calcul.

1. Goh, “Why Momentum Really Works”, Distill, 2017 ↩