Cette dernière décennie a vu une explosion de l’intelligence artificielle (IA) et de ses applications : une croissance exponentielle du nombre d’articles de recherche1, d’entreprises innovantes, d’unités de recherche. L’avènement de l’apprentissage profond (deep learning) a été permis par les améliorations conjointes de la puissance de calcul, des techniques de différenciation automatique, et des architectures de réseaux de neurones artificiels.

Quels sont les algorithmes qui permettent aux machines d’apprendre ?

Gradient

Dans le cas d’une fonction à valeurs réelles, c’est-à-dire dont la sortie a une unique dimension, on peut calculer, en un point, un vecteur bien pratique : le gradient2. Celui-ci se situe dans l’espace de départ de la fonction (son ensemble de définition), et l’opposé de sa direction indique la plus forte pente au point considéré. C’est pourquoi il est naturellement utilisé pour minimiser une fonction : on part d’un point, en général aléatoire, on se déplace dans la direction opposée au gradient, puis on recommence tant qu’il y a assez de pente.

Prenons l’exemple d’une fonction f, définie comme le carré de la norme d’un vecteur en deux dimensions :

Code 
import jax.numpy as jnp
from jax import grad, vmap, jit
import matplotlib.pyplot as plt
import matplotlib.colors as colors

plt.style.use("ggplot")

def make_gradient_field(function, xrange=(-1, 2), yrange=(-1, 2), n_points=30, shape=(2, 1)):
    W = jnp.linspace(*xrange, n_points)
    B = jnp.linspace(*yrange, n_points)
    U, V = jnp.meshgrid(W, B)
    pairs = jnp.dstack([U, V]).reshape(-1, *shape)
    
    vectorized_fun = jit(vmap(function))
    Z = vectorized_fun(pairs).reshape(n_points, n_points)
    
    grad_fun = jit(vmap(grad(function)))
    gradvals = grad_fun(pairs)

    gradx = gradvals[:, 0].reshape(n_points, n_points)
    grady = gradvals[:, 1].reshape(n_points, n_points)

    gradnorm = jnp.sqrt(gradx**2 + grady**2)
    
    return U, V, Z, pairs, gradvals, gradx, grady, gradnorm

def plot_surface(U, V, Z, gradnorm, fig, ax, alpha=0.5, cmap=plt.cm.YlGn):
    scamap = plt.cm.ScalarMappable(cmap=cmap)
    fcolors = scamap.to_rgba(gradnorm)
    
    surf = ax.plot_surface(
        U, V, Z, 
        facecolors=fcolors,
        cmap=cmap,
        alpha=alpha
    )

    clb = fig.colorbar(scamap)
    clb.ax.set_title("Norme du gradient")

def plot_quiver(U, V, gradx, grady, gradnorm, ax, cmap=plt.cm.YlGn):
    q = ax.quiver(U, V, gradx, grady, gradnorm, cmap=cmap)
    clb = fig.colorbar(q)
    clb.ax.set_title("Norme du gradient")
    return ax


def fun(v):
    return jnp.sum(v ** 2)


U, V, Z, pairs, gradvals, gradx, grady, gradnorm = make_gradient_field(
    fun, (-5, 5), (-5, 5), 30, (2,)
)

fig = plt.figure(figsize=(15, 10))
ax = fig.gca(projection="3d")
plot_surface(U, V, Z, gradnorm, fig=fig, ax=ax, alpha=0.7)
plt.xlabel("x")
plt.ylabel("y")
ax.set_zlabel("z")
plt.title("Valeurs prises par la fonction norme au carré") ;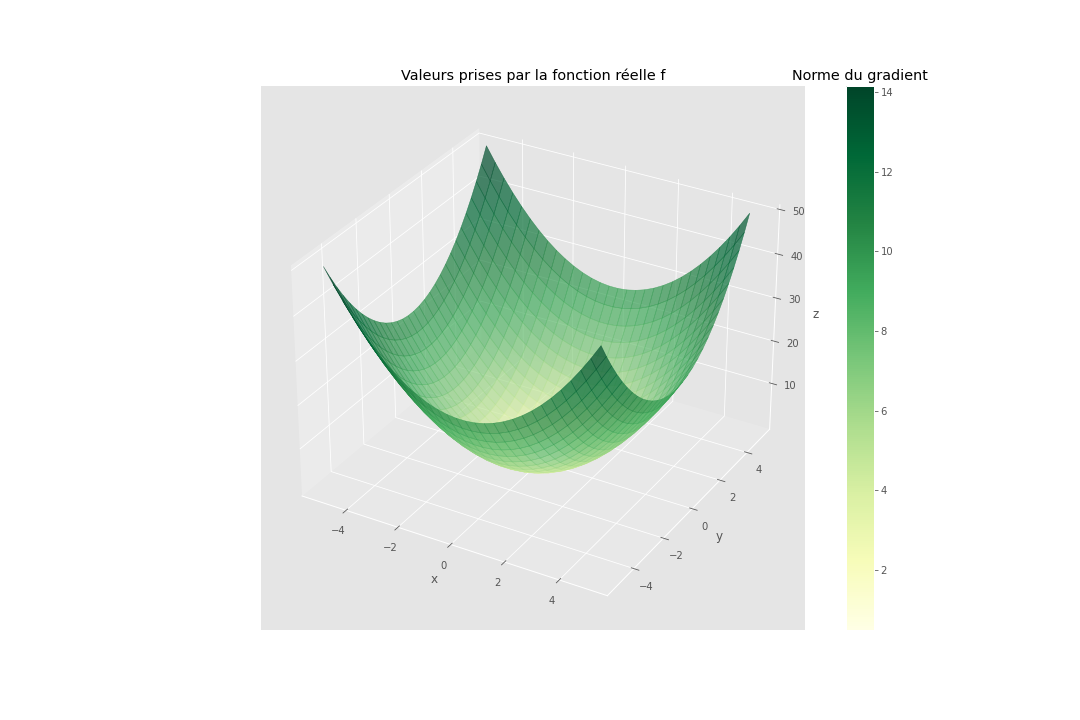
Graphe d'une fonction à deux variables à valeurs réelles
Graphe d'une fonction à deux variables à valeurs réelles. La couleur représente l'intensité (la norme) du gradient

On peut calculer son gradient en tout point, dans l’espace de départ à deux dimensions :

Code 
import pandas as pd

fig, ax = plt.subplots(figsize=(13, 10))
q = ax.quiver(U, V, gradx, grady, gradnorm, cmap=plt.cm.YlGn)
clb = fig.colorbar(q)
clb.ax.set_title("Norme du gradient")
plt.title("Champ vectoriel du gradient de la fonction f\net descente de gradient") ;

grad_fun = grad(fun)
memo = []
x = jnp.asarray([-2., 0.])  # init

for i in range(5):
    memo.append(x)
    g = grad_fun(x)
    x -= g
    
    ax.annotate(
        '', xy=x, xytext=memo[i],
        arrowprops={'arrowstyle': '->', 'color': 'r', 'lw': 2},
        va='center', ha='center'
    )

pd.DataFrame(memo).plot.scatter(0, 1, ax=ax, s=50) ;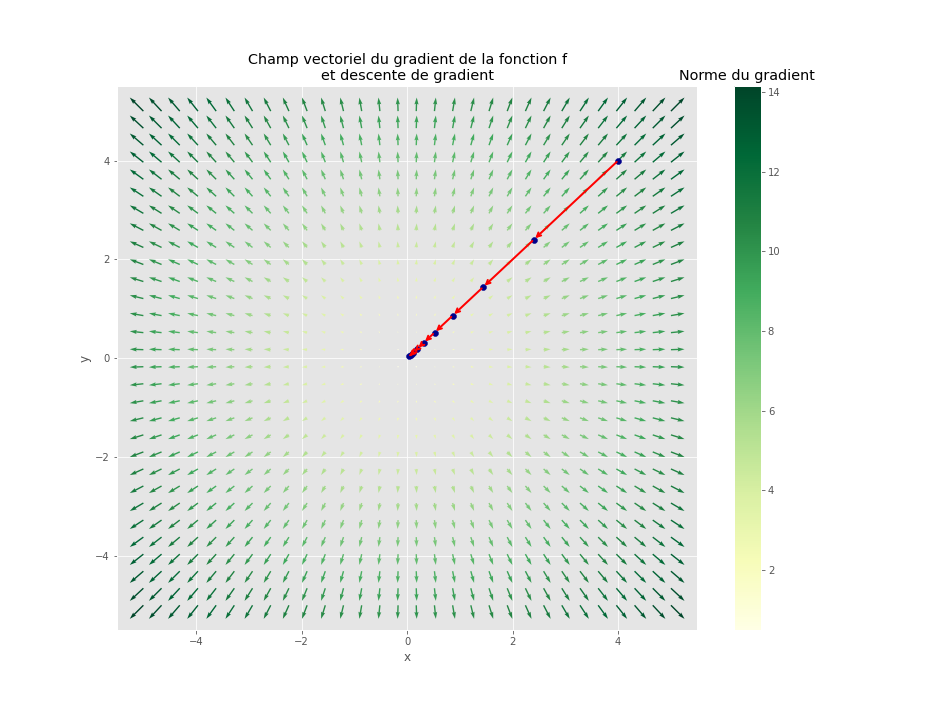
Gradient d'une fonction réelle à deux variables
Champ vectoriel du gradient, et algorithme de descente

Dans le cas illustré ci-dessus, il y a un unique point minimisant la fonction: (0, 0), soit l’origine. On aboutit à proximité de ce point avec une méthode de type descente de gradient quel que soit le point de départ de la descente.

Cette méthode d’optimisation fonctionne très bien dans le cas des fonctions convexes, comme c’est le cas de notre fonction carée, c’est-à-dire que le graphe de la fonction favorise la découverte d’un minimiseur de f. Dans ce cas, on dispose de garanties théoriques que l’algorithme converge vers un minimum global. Pour les fonctions non-convexes, comme c’est le cas des fonctions de coût des réseaux de neurones artificiels profonds3, on ne dispose pas de telles garanties mais on peut tout de même résoudre des problèmes d’optimisation complexes.

Applications

L’application phare de la descente du gradient pendant la dernière décennie, c’est l’apprentissage profond : les réseaux de neurones artificiels. On initialise les neurones avec des poids aléatoires, puis on demande à la machine de minimiser la différence entre ce que l’on souhaiterait que le modèle fasse et ce qu’il fait vraiment. On peut le faire en calculant le gradient de cette opération et en suivant l’algorithme de la descente du gradient, jusqu’à trouver des poids convenables. Cette technique est souvent appelée rétropropagation du gradient, ou backpropagation.

Le récent modèle DALL·E, de l’entreprise OpenAI, permet d’apprécier la puissance de cette technique appliquée aux réseaux de neurones. En l’occurence, il s’agit de générer une image à partir d’une phrase.

Un fauteuil en forme d'avocat
Image générée à partir de la phrase : Un fauteuil en forme d'avocat (le fruit)

L’image ci-dessus n’est pas une photo, ni un dessin, et n’a pas été générée par un logiciel traditionnel nécessitant un travail humain. C’est DALL·E qui l’a créée, ex nihilo.

Avant d’être entraîné avec l’algorithme de la descente de gradient, le modèle fonctionne de la même manière, seulement il génère une image de pixels aléatoires pour n’importe quelle phrase.

Image générée avant entraînement

Deepmind, une entité de Google spécialisée en intelligence artificielle, a de son côté réalisé le modèle AlphaFold, qui a résolu le problème de repliement des protéines de manière automatique, un problème ouvert depuis 50 ans. L’algorithme de la descente de gradient est explicitement mentionné dans un schéma de fonctionement de leur modèle.

Architecture d'Alphafold. source: Deepmind

Ces avancées requièrent donc l’algorithme de la descente de gradient. Mais comment calculer le gradient au juste ? Est-ce que les auteurs de ces programmes disposent d’une formule mathématique qu’ils peuvent implémenter dans un langage de programmation classique ?

AutoDiff

La différenciation automatique (AutoDiff, ou AD) consiste à calculer les dérivées, d’ordre 1 ou supérieur, d’une fonction encodée dans un langage de programmation adapté4.

Cette approche se distingue de:

  • la différenciation symbolique (calcul formel ou CAS)
  • la différenciation numérique (méthode des différences finies)

La différenciation numérique est parfois instable numériquement. La différenciation symbolique, quant à elle, conduit à un gonflement de la taille des expressions, et n’est pas capable de différencier des instructions de structure de contrôle (if, for etc.)5. Ces deux méthodes sont également gourmandes en calculs. L’AD est, parmi ces trois options, le système qui convient pour l’apprentissage automatique (machine learning)6,7.

Pour implémenter l’AD, on définit d’abord les règles de dérivation des opérations élémentaires, appellées primitives : addition, multiplication, exponentielle, sinus etc. En mémorisant la suite des transformations appliquées successivement aux paramètres d’entrée d’une fonction quelconque, et à l’aide de la règle de la chaîne, un algorithme peut calculer la valeur numérique exacte (avec une précision machine) de la dérivée en n’importe quel point.

En Python, il y a plusieurs systèmes d’AD, qui se sont développés avec l’apprentissage profond. Les plus connus sont:

  • GradientTape de Tensorflow (TF) par Google
  • Autograd de PyTorch (par Facebook)
  • JAX8 par Google également

Nous avons ici utilisé JAX. On peut par exemple calculer les dérivées d’ordres 1 et supérieur (2, 3) de fonctions pures:

Code 
x = jnp.linspace(-3, 3, num=100)

f = jnp.square

for i in range(3):
    f_vect = vmap(f)  # vectorize function
    plt.plot(x, f_vect(x), label=i)
    f = grad(f)  # next derivative

plt.title(f"Dérivées successives de la fonction carrée avec AutoDiff (JAX)")
plt.xlabel("x")
plt.legend() ;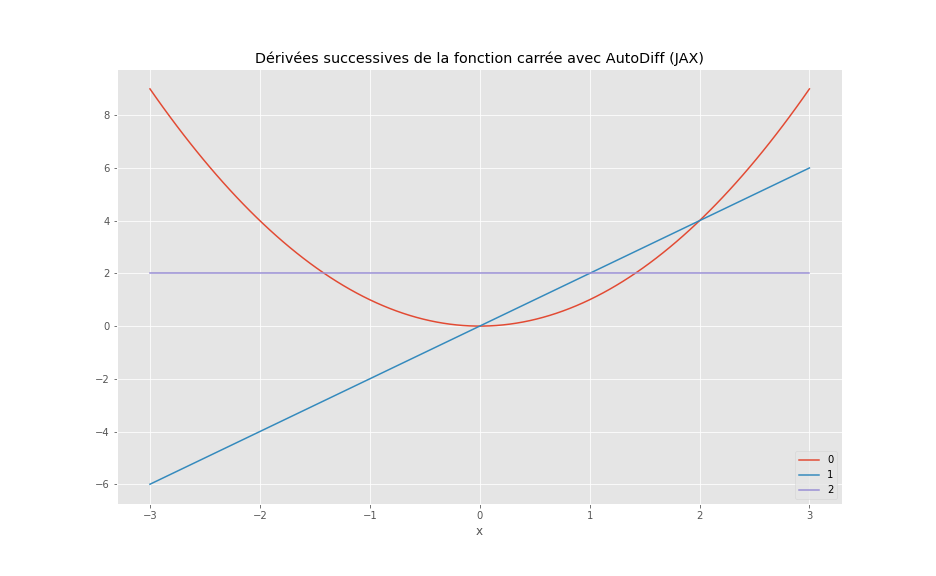
Différenciation automatique de la fonction carrée
Différenciation automatique d'ordres supérieurs

JAX emploie la méthode de traçage pour calculer le gradient. Lorsque python invoque la fonction grad, le programme exécute d’abord les instructions pour calculer le résultat de la fonction, tout comme un programme classique. Ensuite, il analyse les opérations effectuées pour générer des instructions qui calculent le gradient de cette fonction.

Ci-dessous, nous pouvons voir les instructions machines et le graphe des opérations, générés par JAX, pour calculer le gradient de la fonction (scalaire) carrée:

Code 
# Source: https://gist.github.com/niklasschmitz/559a1f717f3535db0e26d0edccad0b46

import jax
from jax import core
from graphviz import Digraph
import itertools
import jax.numpy as jnp


styles = {
    "const": dict(style="filled", color="goldenrod1"),
    "invar": dict(color="mediumspringgreen", style="filled"),
    "outvar": dict(style="filled,dashed", fillcolor="indianred1", color="black"),
    "op_node": dict(shape="box", color="lightskyblue", style="filled"),
    "intermediate": dict(style="filled", color="cornflowerblue"),
}


def _jaxpr_graph(jaxpr):
    id_names = (f"id{id}" for id in itertools.count())
    graph = Digraph(
        engine="dot",
    )
    graph.attr(size="6,10!")
    for v in jaxpr.constvars:
        graph.node(str(v), core.raise_to_shaped(v.aval).str_short(), styles["const"])
    for v in jaxpr.invars:
        graph.node(str(v), v.aval.str_short(), styles["invar"])
    for eqn in jaxpr.eqns:
        for v in eqn.invars:
            if isinstance(v, core.Literal):
                graph.node(
                    str(id(v.val)),
                    str(v.val),
                    styles["const"],
                )
        if eqn.primitive.multiple_results:
            id_name = next(id_names)
            graph.node(id_name, str(eqn.primitive), styles["op_node"])
            for v in eqn.invars:
                graph.edge(
                    str(id(v.val) if isinstance(v, core.Literal) else v), id_name
                )
            for v in eqn.outvars:
                graph.node(str(v), v.aval.str_short(), styles["intermediate"])
                graph.edge(id_name, str(v))
        else:
            (outv,) = eqn.outvars
            name = "\n".join([str(eqn.primitive), str(eqn.params or "")])
            graph.node(str(outv), name, styles["op_node"])
            for v in eqn.invars:
                graph.edge(
                    str(id(v.val) if isinstance(v, core.Literal) else v), str(outv)
                )
    for i, v in enumerate(jaxpr.outvars):
        if i == 0:
            outv = "value"
        else:
            outv = "gradient"
        graph.node(outv, outv, styles["outvar"])
        graph.edge(str(v), outv)
    return graph


def jaxpr_graph(fun, *args):
    jaxpr = jax.make_jaxpr(fun)(*args).jaxpr
    return _jaxpr_graph(jaxpr)


def square(x):
    acc = 1
    for i in range(2):
        acc *= x
    return acc


f = jax.value_and_grad(square)
x = jnp.array(2.2)
jaxpr = jax.make_jaxpr(f)(x).jaxpr
print(jaxpr)
graph = jaxpr_graph(f, x)
graph.attr(size="8,5")
graph
{ lambda  ; a.
  let b = mul a 1.0
      c = mul b a
      d = mul 1.0 b
      e = mul 1.0 a
      f = mul e 1.0
      g = add_any d f
  in (c, g) }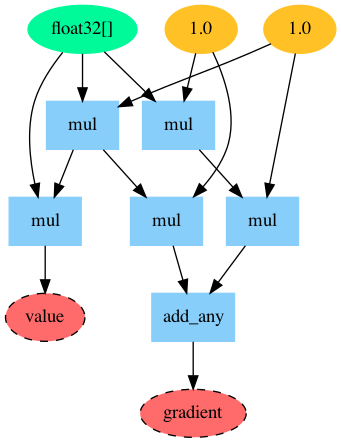
Graphe de calculs permettant à JAX de calculer la valeur et le gradient d'une fonction en un point
Représentation intermédiaire (JAXPR) de la fonction carée

Implémentations

Les outils en Python sont puissants, mais limités dans un certain sens : Python étant un langage très dynamique, interprété, et relativement lent, il est difficile de calculer rapidement le gradient de fonctions écrites avec des structures de contrôle habituelles, soit if, for etc., et avec des structures de données habituelles, c’est à dire des listes, tuples, dictionnaires etc. Pour contrer cela, il faut implémenter la fonction que l’on souhaite différencier dans un système adapté, utilisant souvent des structures de données de type tableaux multidimensionnels.

Pour programmer un réseau de neurones avec Tensorflow (TF), il faut ainsi utiliser les structures de données TF, les opérations (somme, multiplication, tanh etc.) TF, et ainsi créer son code spécifiquement pour qu’il fonctionne avec ce framework. JAX est un peu plus flexible, mais ne fait pas exception à la règle en ce qu’il réimplémente quasi-entièrement la bibliothèque numpy dans jax.numpy pour être compatible avec l’AD (le lecteur attentif aura remarqué la substitution de np par jnp dans le code ci-dessus).

D’autres approches plus holistiques promettent plus de flexibilité. On peut notamment citer le langage Julia, dans lequel on peut différencier des fonctions opérant sur des structures de données standard avec un code standard avec les outils actuels9, ce qui tranche avec les structures de données spécifiques à chaque librairie en python. Il y a au moins une dizaine de librairies en Julia qui rentrent dans la catégorie AD5.

D’autre part, le jeune programme Enzyme peut différencier tout code compilé avec LLVM. Enzyme travaille directement avec la réprésentation LLVM IR, ce qui lui donne le bénéfice des optimisations faites par le compilateur. Cela donne, en théorie, accès au gradient de fonctions écrites dans tous les langages qui ont une implémentation utilisant LLVM, soit notamment C, C++, Fortran, Haskell, Julia, Rust, Swift…

Certains gros acteurs expérimentent activement dans ces directions. On peut citer Google qui, après Tensorflow et JAX, a lancé Swift for Tensorflow en 2017, une implémentation d’AutoDiff qui s’applique à tout le language Swift. Certains chercheurs, dont les auteurs originaux de JAX et PyTorch, travaillent également actuellement sur Dex10, un nouveau langage de programmation adapté aux manipulations de données, en visant notamment la différentiabilité.

D’autres expérimentations sont nées récemmment dans ce domaine11,12, ouvrant la voie au paradigme de la programmation différentiable.

Sources et références

  1. Evolution dans le temps du nombre de publications sur l’IA ↩

  2. Dans le cas d’une dimension unique, le gradient est égal à la dérivée ↩

  3. Bach, Global convergence of gradient descent for non-convex learning problems ↩

  4. Baydin et al., Automatic differentiation in machine learning: a survey ↩

  5. JuliaDiff, Stop approximating derivatives ↩ ↩2

  6. Justin Domke, Automatic Differentiation: The most criminally underused tool in the potential machine learning toolbox? (2009) ↩

  7. Radul, Introduction to automatic differenciation ↩

  8. Deepmind, Using JAX to accelerate our research ↩

  9. Innes et al., ∂P: A Differentiable Programming System to Bridge Machine Learning and Scientific Computing ↩

  10. Maclaurin & al., Dex: array programming with typed indices ↩

  11. Autodiff pour F#, Diffsharp: differentiable tensor programming made simple ↩

  12. Github issue, Supporting algorithmic differentiation (AD) in the Futhark language and compiler ↩